| ACCUEIL | Le module turtle | DECOUVERTE | APPLICATION | EVALUATION |
Applications du module turtle
En utilisant les instructions de la tortue données sur la page découverte, proposez un programme pour chacune des applications suivantes.
Les applications à réaliser correspondent chacune à une figure graphique :
Application 1 : l'étoile à 5 branches
Application 2 : le coeur, le carreau, le trèfle et le pique
Application 3 : les rosaces colorées
Application 4 : les triangles imbriqués
Application 1 : l'étoile à 5 branches
Proposez un programme qui trace une étoile à 5 branches régulière dans la fenêtre de la tortue :

Voici pour information quelques éléments géométriques de l'étoile à 5 branches :
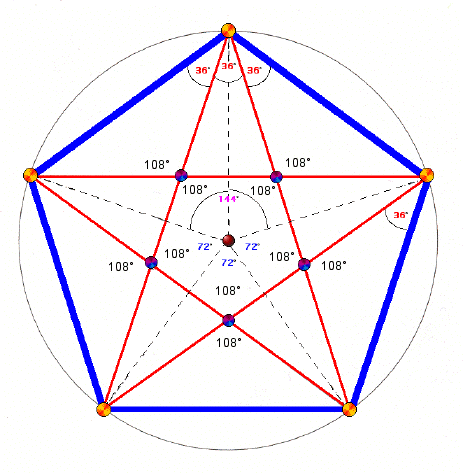
Remarques concernant les angles particuliers de l'étoile à 5 branches sachant que l'angle plein vaut 360° :
360°/5 = 72°
360°/(2*5) = 36°
(2*360°)/5 = 144°
144° - 36° = 108°
Méthode de travail demandée :
- ÉTAPE 1 : vous recherchez expérimentalement dans IPython les différentes instructions permettant de tracer l'étoile à 5 branches
- ÉTAPE 2 : vous enregistrerez dans EduPython votre programme final dans un fichier nommé etoile.py
Application 2 : le cœur
Proposez un programme qui trace un cœur dans la fenêtre de la tortue, constitué de 2 segments et de 2 arcs de cercle parfaitement joints :

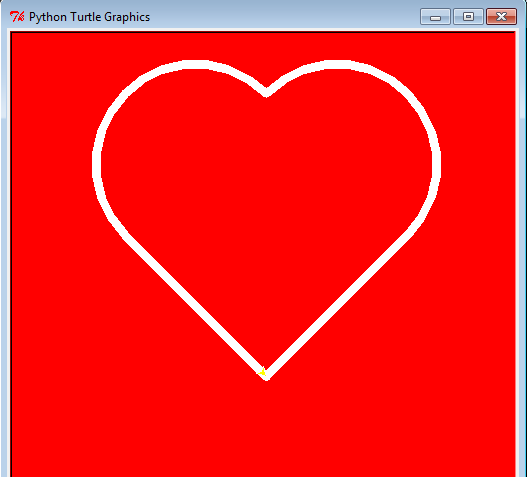
Rappel de la méthode de travail demandée :
- ÉTAPE 1 : vous recherchez expérimentalement dans IPython les différentes instructions permettant de tracer le coeur
- ÉTAPE 2 : vous enregistrerez dans EduPython votre programme final dans un fichier nommé coeur.py
Suite de l'application 2 : cœur carreau trèfle pique
Enregistrez votre programme coeur.py dans un nouveau fichier nommé pique.py
Améliorez votre programme du cœur afin de rajouter dans la fenêtre de la tortue un carreau, un trèfle et un pique.
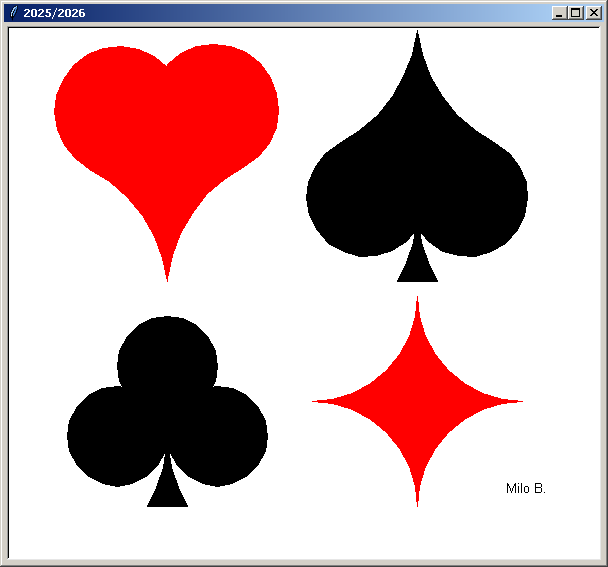
Voici un modèle représentant les 4 figures à reproduire avec la tortue. On peut remarquez qu'en utilisant un grand nombre d'arcs de cercle (à la place de simples segments de droite) les figures sont plus réalistes :
L'ordre des 4 figures est libre, mais vous veillerez à ce que :
- les 2 figures rouges (le cœur et le carreau) soient sur une des diagonales
- les 2 figures noires (le trèfle et le pique) soient sur l'autre diagonale
- le trèfle et le pique doivent être assortis : ils doivent notament avoir le même pied
- les 4 figures doivent avoir la même hauteur et doivent être alignées
- les 4 figures doivent être droite et parfaitement symétriques
- si on enchaîne un segment droit et un arc de cercle il faut une continuité parfaite sans cassure (par exemple pour le cœur)
- la marge entre les figures et le bord de la fenêtre de la tortue doit être constante et régulière (la même à droite, à gauche, en haut et en bas)
- le fond de la fenêtre doit rester blanc
- les 2 figures rouges (le cœur et le carreau) doivent être entièrement colorées en rouge (les traits comme le fond de la figure)
- les 2 figures noires (le trèfle et le pique) doivent être entièrement colorées en noir (les traits comme le fond de la figure)
- vous avez une liberté dans la forme des figures, mais aucune liberté concernant les couleurs
Voici quelques exemples obtenus avec la tortue en Python. Il ne s'agit là que d'exemples réalisés les années précédentes, aucun n'est parfait, il ne s'agit pas de modèle à reproduire tel quel. Observer bien les détails et suppimer les défauts que vous constatez :

Problème au niveau du cœur : il y a une cassure entre le segment et l'arc de cercle
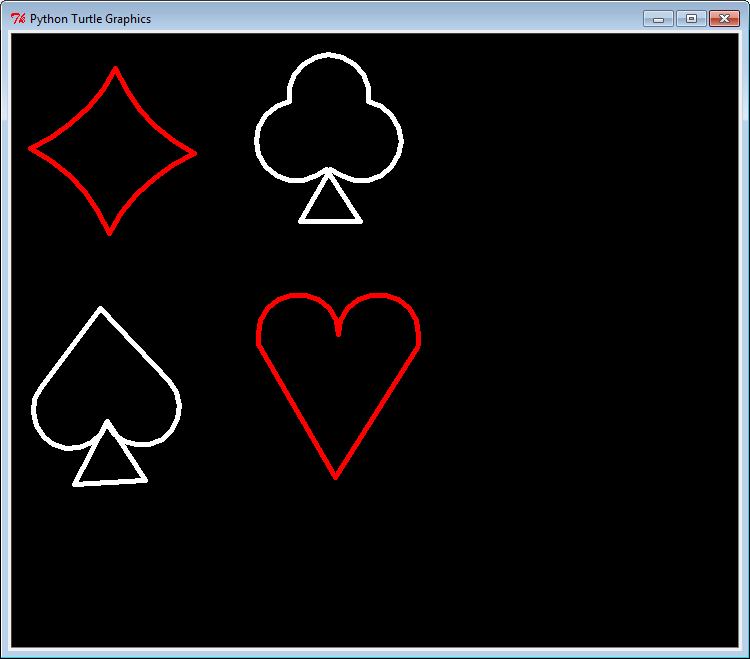
Problème au niveau du cœur : il y a une cassure entre le segment et l'arc de cercle.
De plus les figures ne sont pas correctement réparties dans la fenêtre et le pique n'est pas droit

Le pied du trèfle est trop large, et ses 3 feuilles ne sont pas assez développées

Le pied du trèfle est trop large, et ses 3 feuilles ne sont pas assez développées

Le trèfle et le pique n'ont pas le même pied

Le cœur, le carreau et le trèfle sont très beaux, mais le pique doit être plus soigné et :
le fond de la fenêtre doit rester blanc et les 4 figures doivent être colorées entièrement
Figures créées en 2024/2025 :

Le trèfle et le pique n'ont pas le même pied

Le trèfle et le pique n'ont pas le même pied

Le carreau est un peut plus haut que les 3 autres figures
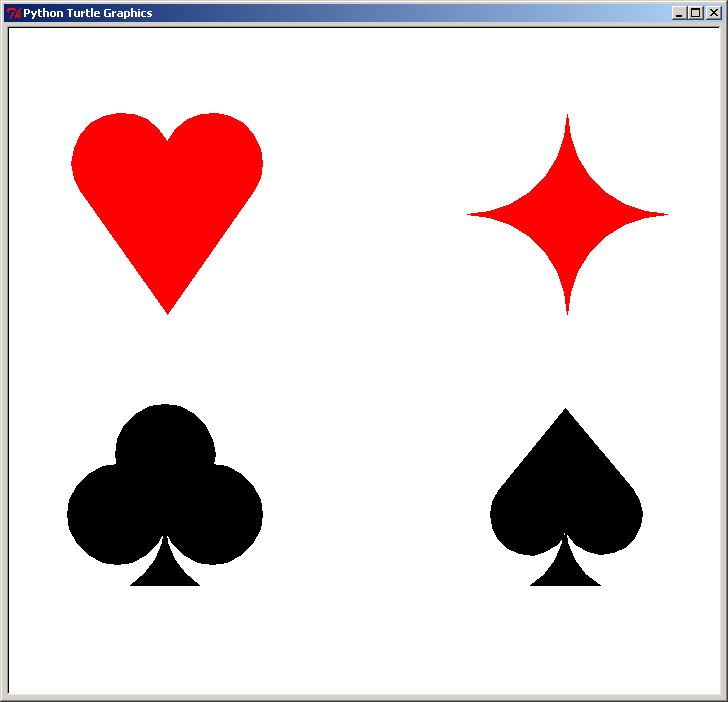
Belles figures, bonne répartition dans la fenêtre, même pied pour le trèfle et pour le pique mais :
les 2 figures rouges doivent être sur une diagonale et les 2 figures noires sur l'autre diagonale

Belles figures assorties, mais les feuilles du trèfles doivent être plus développées

Très beau trèfle mais le fond de la fenêtre doit reste blanc afin de bien faire ressortir les 4 figures (ici on ne voit que le rose)

Le cœur et le carreau doivent être colorés en rouge, le trèfle et le pique doivent être colorés en noir
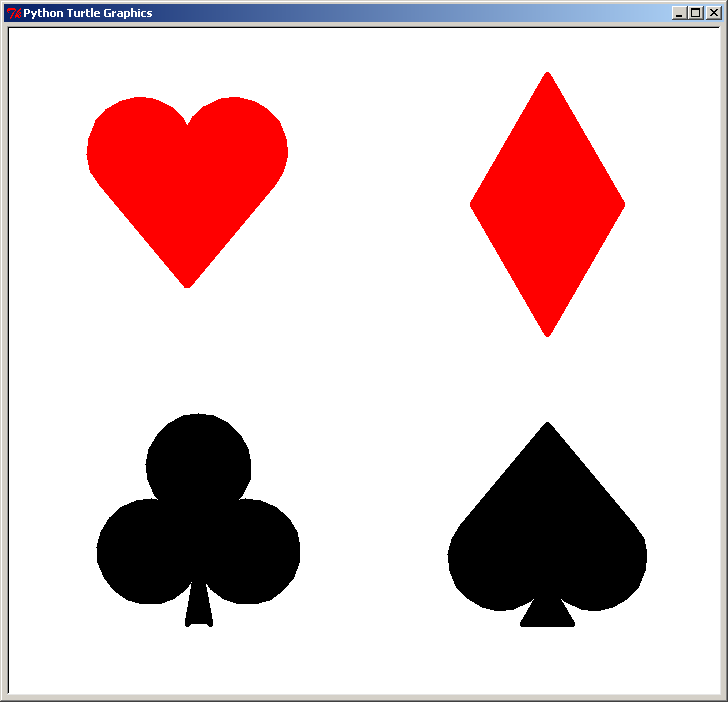
Les feuilles du trèfles sont bien développées, mais son pied n'est pas le même que celui du pique, et
les 2 figures rouges doivent être sur une diagonale et les 2 figures noires sur l'autre diagonale
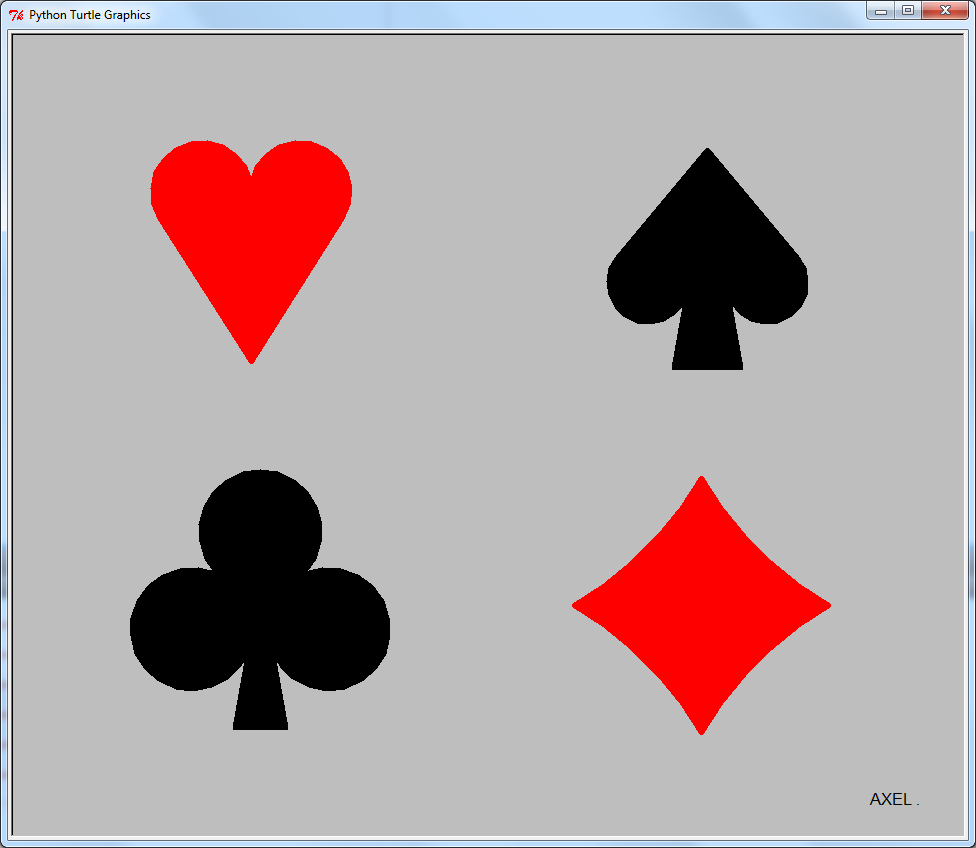
Les feuilles du trèfles sont bien développées, mais son pied n'est pas le même que celui du pique qui peut être amélioré
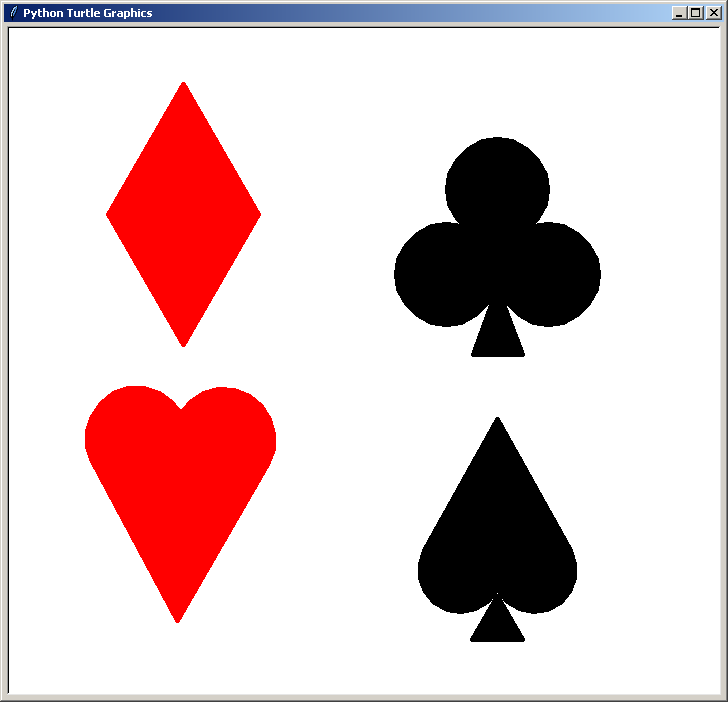
Le carreau et le trèfle n'ont pas la même hauteur, et
les 2 figures rouges doivent être sur une diagonale et les 2 figures noires sur l'autre diagonale
Nouvelles figures créées en 2025/2026 :

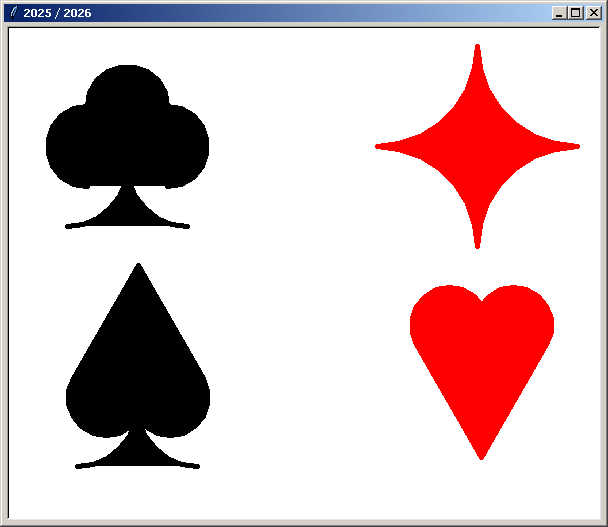





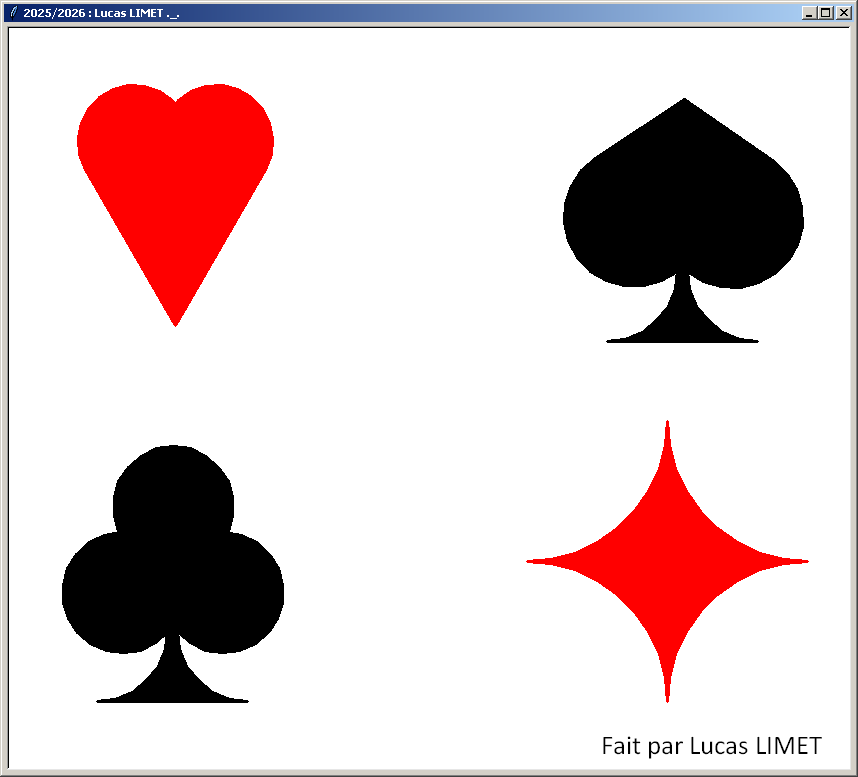
Rappel de la méthode de travail demandée :
- ÉTAPE 1 : vous recherchez expérimentalement dans IPython les différentes instructions permettant de tracer un carreau, un trèfle et un pique (en plus du coeur)
- ÉTAPE 2 : vous enregistrerez dans EduPython votre programme final dans un fichier nommé pique.py
Vous structurerez votre programme pique.py comme indiqué ci-dessous, en créant une fonction pour chaque figure (coeur, carreau, trèfle et pique) ainsi qu'un fonction deplacer(x,y) permettant de déplacer le curseur aux coordonnées (x,y) en levant le crayon et sans tracer de trait :
# ----------------------------------------------------------------------------
# Programme pique.py qui trace les 4 figures : coeur, carreau, trèfle et pique
# ----------------------------------------------------------------------------
# importation du module turtle :
from turtle import *
# ----------------------------------------------------------------------------
# Déclaration des fonctions
# ----------------------------------------------------------------------------
# fonction coeur() qui trace la figure coeur :
def coeur():
color('red')
pensize(6)
left(120)
forward(150)
left(180)
circle(60,-200)
etc.
# fonction carreau() qui trace la figure carreau :
def carreau():
color('red')
pensize(6)
left(60)
forward(150)
right(120)
forward(150)
right(60)
forward(150)
right(120)
forward(150)
# fonction trefle() qui trace la figure trèfle :
def trefle():
color('black')
pensize(6)
???
# fonction pique() qui trace la figure pique :
def pique():
color('black')
pensize(6)
???
# fonction deplacer(x,y) qui déplace le curseur sans tracer de trait entre 2 figures :
def deplacer(x,y):
# lève le crayon :
up()
# déplace le curseur au point de coordonnées (x,y) :
goto(x,y)
# baisse le crayon :
down()
# ----------------------------------------------------------------------------
# Programme principal
# ----------------------------------------------------------------------------
# configure la taille de la fenêtre :
setup(800,800)
# donne un titre à la fenêtre pour la signer (prénom + année scolaire):
title('Balthazar 2025/2026')
# efface le curseur de la tortue :
hideturtle()
# trace en vitesse rapide :
speed(0)
# trace les 4 figures en appelant les différentes fonctions :
deplacer(-200,200)
coeur()
deplacer(200,200)
carreau()
deplacer(-200,-200)
trefle()
deplacer(200,-200)
pique()
# libère la fenêtre de la tortue :
done()
IMPORTANT : les valeurs en bleu dans le programme ci-dessus sont à adapter ou à compléter. Cet exemple vous donne seulement la structure de votre programme (liste et nom des fonctions à créer, séparation entre la déclaration des fonctions et le programme principal) et non ses instructions exactes.
Application 3 : tracé d'une rosace
Dans cette application on va demander à la tortue de Python de tracer une rosace exactement comme on l'aurait fait au compas sur le papier. Nous complexifirons ensuite la rosace, aussi bien en couleurs qu'en nombre de pétales.
La rosace sera créée en 3 exemplaires qui vont se complexifier profressivement :
- rosace version 1 : la rosace de base à 6 pétales (enregistrée dans un fichier nommé rosace_v1.py)
- rosace version 2 : la rosace colorée (enregistrée dans un fichier nommé rosace_v2.py)
- rosace version 3 : la rosace complexe composées de plusieurs rosaces (enregistrée dans un fichier nommé rosace_v3.py)
Voici un apperçu rapide du résultat attendu pour chacune des 3 versions de la rosace :
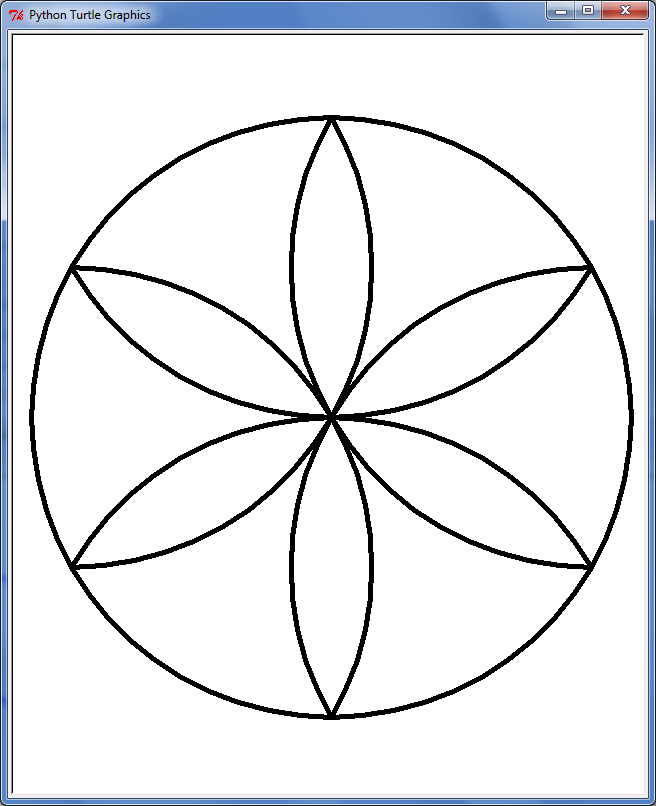
la rosace de base : programme rosace_v1.py

exemple de rosace colorée : programme rosace_v2.py
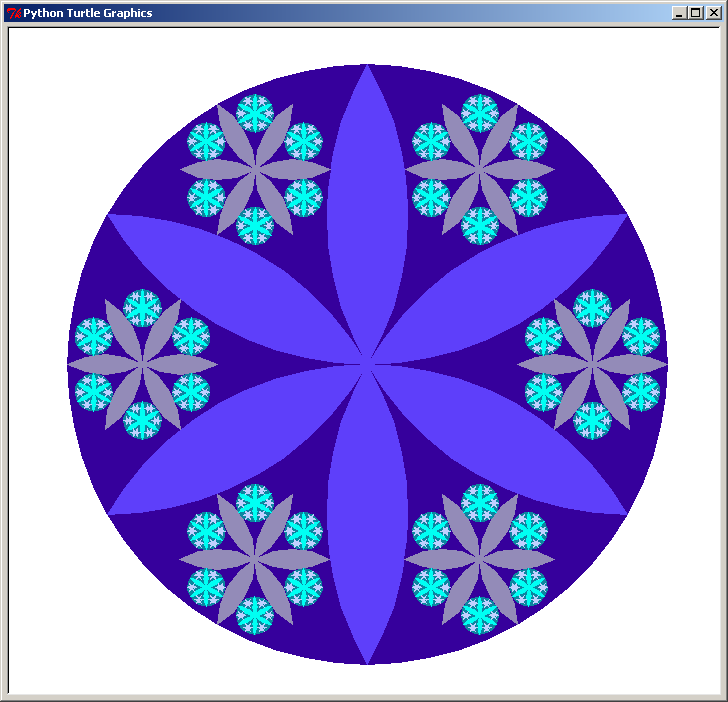
exemple de rosace complexe : programme rosace_v3.py
Suivez maintenant les instructions ci-dessous pour créer progressivement chacune des 3 rosaces.
La rosace version 1 : rosace de base
Cette première version est une rosace simple, composée de 6 pétales, sans couleur, et représentant exactement le mêm résultat qu'une rosace tracée au compas sur le papier.
Voici le résultat attendu pour la rosace version 1 :

Et voici l'algorithme qui a permis d'obtenir cette rosace simple. Un algorithme donne les instructions à réaliser, avec des phrases simples en français. Pour obtenir la rosace il vous appartient de convertir cet algorithme en programme Python en remplaçant les indications données par des instructions Python équivalentes et permettant de piloter la tortue.
Dans ces algorithmes la variable R est le rayon de la rosace. Utilisez par exemple R=300
Algorithme 1 de la rosace simple non colorée |
|
Voici un autre algorithme donnant le même résultat au final :
Algorithme 2 de la rosace simple non colorée |
|
En utilisant un des deux algorithmes au choix, proposez un programme qui trace une rosace dans la fenêtre de la tortue.
Rappel de la méthode de travail demandée :
- ÉTAPE 1 : vous testez expérimentalement dans IPython les différentes instructions correspondant à l'algorithme jusqu'à réussir à tracer une rosace parfaite
- ÉTAPE 2 : vous enregistrerez dans EduPython votre programme final dans un fichier nommé rosace_v1.py en y rassemblant seulement les instructions utiles
Une fois la rosace de base terminée, ajoutez le titre suivant à votre programme rosace_v1.py pour signer votre création dans la barre de titre de la fenêtre de la tortue :
title('2025/2026 : rosace version 1')
Votre programme rosace_v1.py est totalement terminé si :
- il possède un titre comme indiqué ci-dessus
- il trace la rosace en vitesse rapide : speed(0)
- le curseur de la tortue est caché : hideturtle()
- la rosace a un rayon de 300
- la rosace est centrée dans la fenêtre de la tortue qui doit garder sa taille par défaut
La rosace version 2 : coloriage de la rosace
L'algorithme du programme de la rosace version 2 étant totalement différente de la rocase de base version 1, repartez d'un nouveau programme que vous appellerez rosace_v2.py.
L'objectif de cette version 2 est de pouvoir colorer la rosace avec une couleur différentes par pétale (ce qui n'était pas le cas dans la rosace version 1 car les pétales étaient dessinnés 3 par 3).
Voici quelques exemples du résultat attendu :
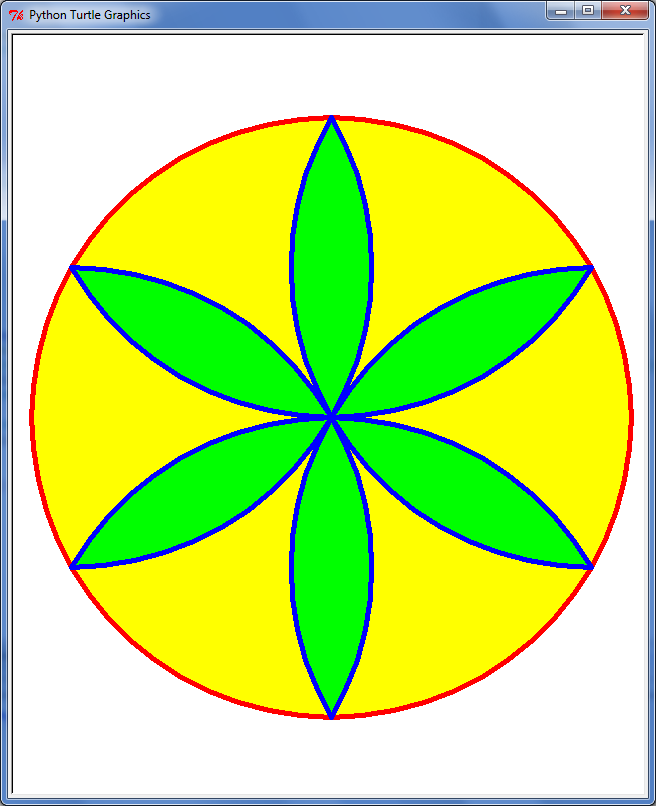
Pour l'instant, tous les pétales ont la même couleur

Voici une rosace à 6 pétales avec une couleur différentes pour chaque pétales
Pour obtenir une rosace simple (rosace de base à 6 pétales comme la précédente) dont chaque surface fermée est colorée, vous pouvez suivre cet algorithme :
Algorithme de la rosace colorée |
|
Rappel : pour utiliser 16 millions de couleurs différentes on peut indiquer directement le code numérique des couleurs en hexadécimal à la fonction color (chaîne de caractères commençant par #).
Exemple pour configurer à la fois la couleur du trait et la couleur du remplissage (instructions indiquées en rouge dans l'algorithme ci-dessus) :
color('#F8E204','#D3FC15')
Pour obtenir la valeur numérique d'une couleurs parmi les 16 millions de couleurs possibles, cliquez ici pour ouvrir le nuancier de couleur.
L'idée est ensuite de complexifier la rosace, en lui ajoutant des pétales suplémentaires.
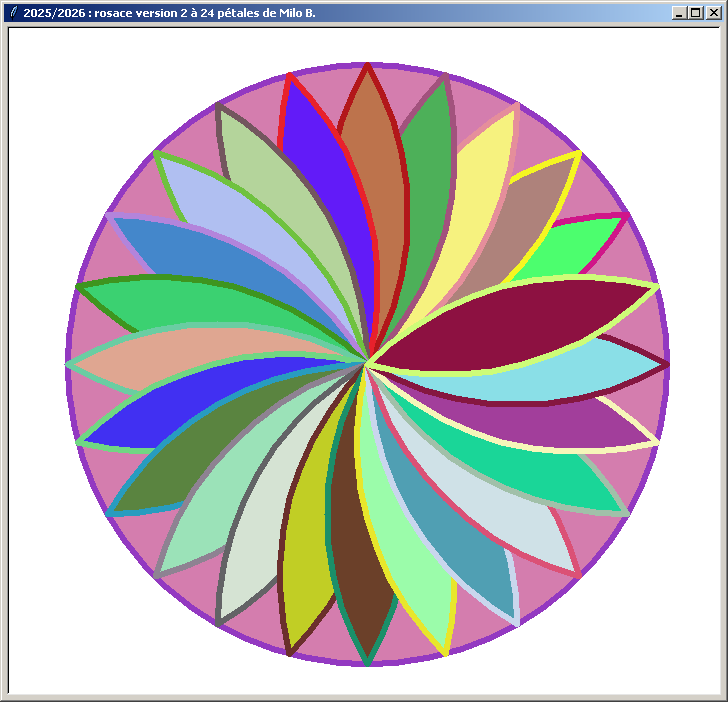
Voici quelques exemples de résultats obtenus pour la rosace version 2 :

Une rosace colorée à 12 pétales

Une rosace colorée à 18 pétales
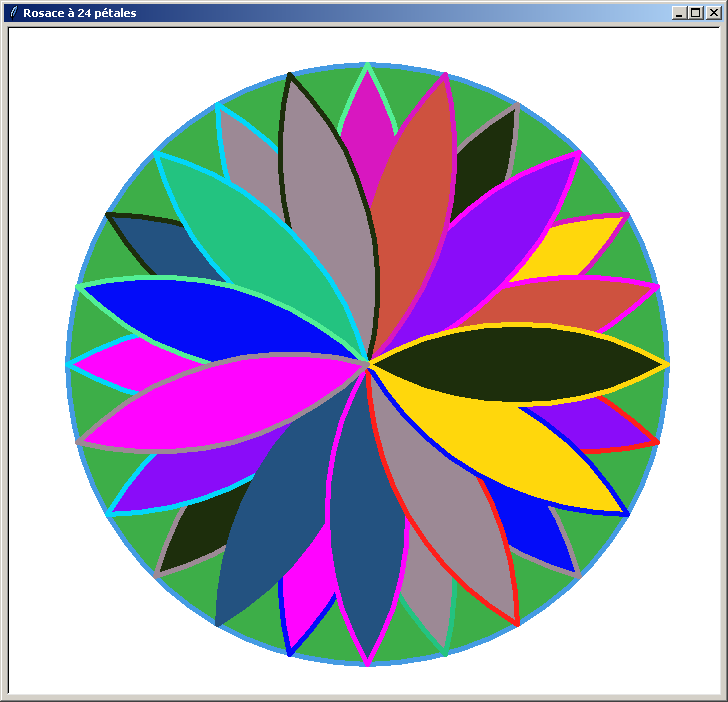
Une rosace colorée à 24 pétales

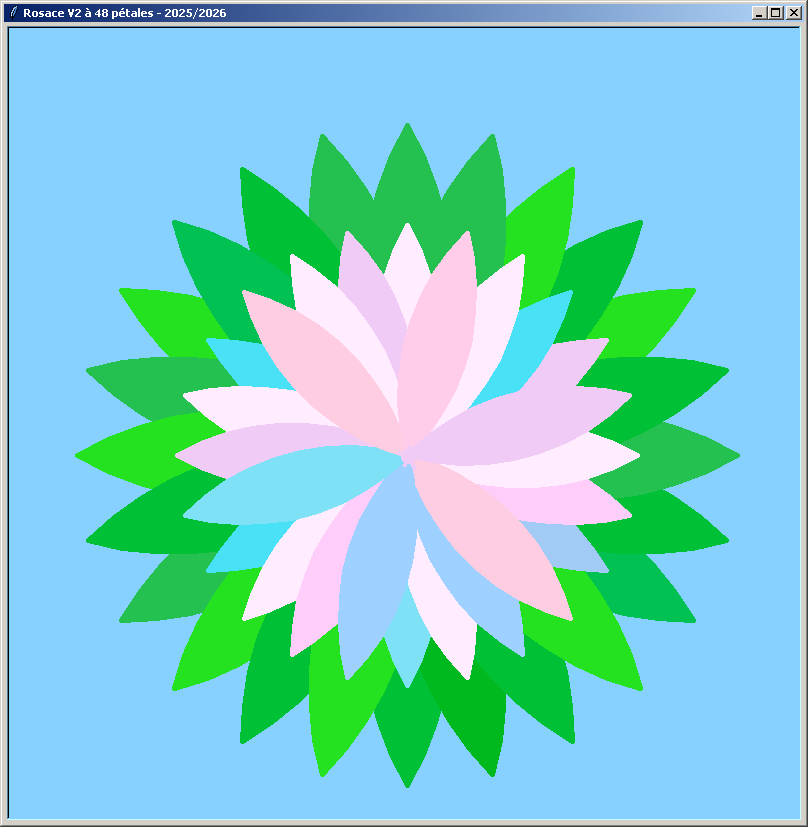
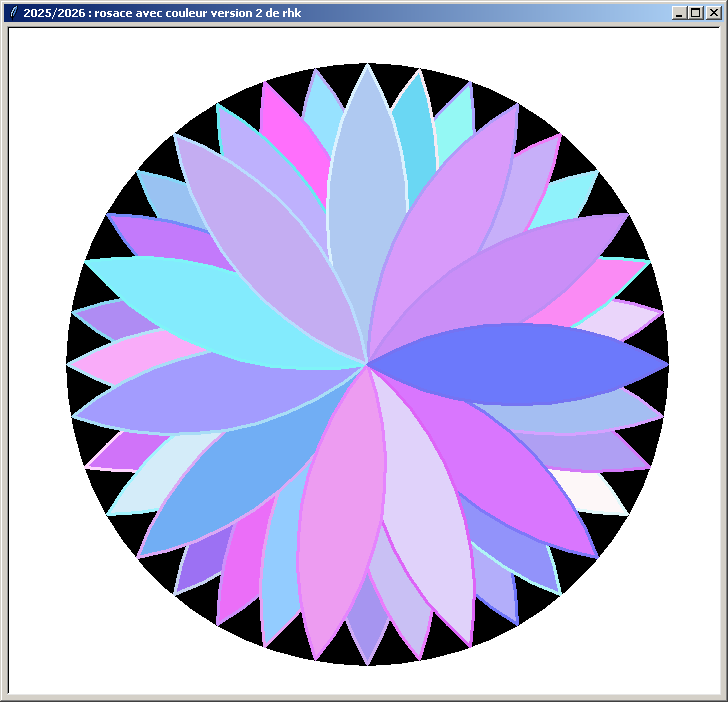
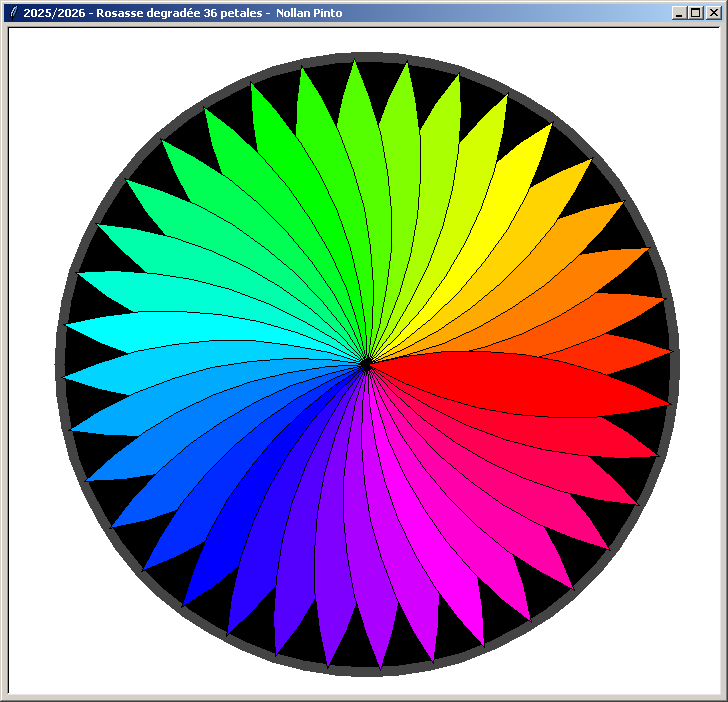
Une rosace colorée à 36 pétales
Une fois que vous avez une rosace (à 6 pétales ou plus) avec une couleur différente pour chaque pétale, enregistrez votre programme rosace_v2.py en y ajoutant le titre suivant afin de signer votre création dans la barre de titre de la fenêtre de la tortue, puis passez à la version 3 :
title('2025/2026 : rosace version 2')
Rappel : votre programme rosace_v2.py est totalement terminé si :
- il possède un titre comme indiqué ci-dessus
- il trace la rosace en vitesse rapide : speed(0)
- le curseur de la tortue est caché : hideturtle()
- la rosace a un rayon de 300
- la rosace est centrée dans la fenêtre de la tortue qui doit garder sa taille par défaut
La rosace version 3 : rosace complexe
Pour cette version 3 de la rosace on va utiliser les fonctions afin de dessiner plusieurs fois la même figure sans répéter le code source.
La structure du programme de la rosace version 3 étant totalement différente des rocases de base, repartez d'un nouveau programme que vous appellerez rosace_v3.py.
On rappelle qu'une rosace est avant tout un ensembles de pétales (et non un ensemble de cercles) répartis circulairement : un pétale étant composé de 2 arcs de cercle.
Étape 1 : on va créer une fonction petale(rayon,orientation) à qui on passe en paramètre le rayon ainsi que l'orientation du curseur avant de dessiner le pétale. Un pétale est une figure composée de 2 arcs de cercle de rayon R. En appelant plusieurs fois la fonction petale(rayon,orientation) on peut dessiner plusieurs pétales correctement répartis, de plus en plus petits et de plus en plus nombreux. Voici un exemple de résultat obtenu :

Cette figure est un ensemble de pétales : c'est bien une rosace
Étape 2 : on va ajouter à notre programme une fonction rosace(R,c1,c2,c3) à qui on passe en paramètre le rayon R ainsi que 3 couleurs :
- c1 pour la couleur du fond du rond principal (dessiné sous les pétales, donc dessiné avant les pétales)
- c2 pour la couleur du trait des pétales (2 arcs de cercle)
- c3 pour la couleur du fond des pétales
Une rosace est une figure composée de 6 pétales dessinés sur un cercle entier de rayon R : la fonction rosace(R,c1,c2,c3) doit donc appelé plusieurs fois la fonction petale(rayon,orientation).
En appelant plusieurs fois la fonction rosace(R,c1,c2,c3) on peut dessiner plusieurs rosaces correctement répartis et de plus en plus petites.
Important : dans cette version 3 toutes les rosaces et sous-rosaces auront 6 pétales (pas plus) et les 6 pétales ont tous la même couleur pour une rosace donnée.
L'important ici est de jouer sur la complexité de la figure et appelant plusieurs fois la fonction rosace(R,c1,c2,c3) afin de répartir régulièrement les sous-rosaces de taille de plus en plus petite.
Plus les rosaces sont petites, plus le trait des pétales doit être fin. Pour les rosaces les plus petites la couleur du trait sera la même que la couleur du fond pour les pétales (c2 et c3 identiques).
Voici quelques exemples de résultats obtenus pour la rosace version 3 :

Cette figure est un ensemble de rosaces de taille différentes

Cette figure est un ensemble de rosaces de taille différentes

Cette figure est un ensemble de rosaces de taille différentes

Chaque rosace et sous-rosace ont ici la même couleur

Chaque rosace et sous-rosace ont ici des couleurs différentes
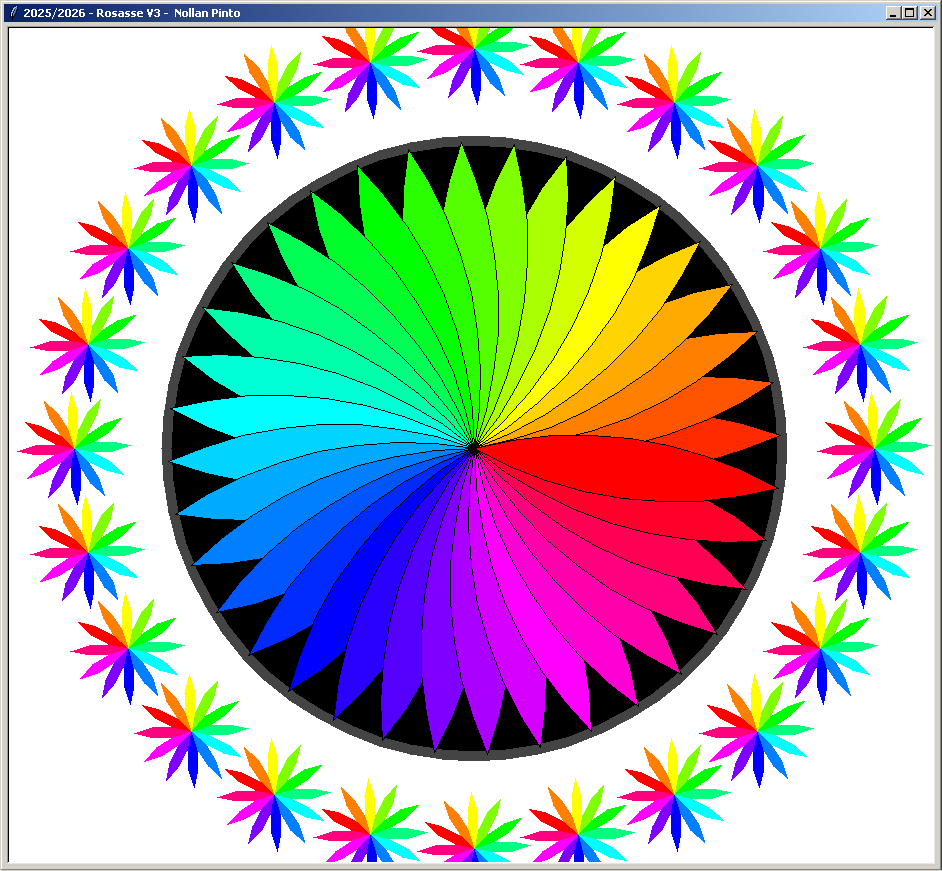
Ici les sous-rosaces font le tour de la rosace principale, et en plus on joue avec les dégradés de couleur
Voici la structure de base du programme rosace_v3.py pour tracer la rosace version 3. Ce programme est composé des 2 fonctions petale(rayon,orientation) et rosace(R,c1,c2,c3) qu'il vous reste à compléter :
# ----------------------------------------------------------------------------
# Programme rosace_v3.py qui trace une rosace complexe
# ----------------------------------------------------------------------------
# importation du module turtle :
from turtle import *
# ----------------------------------------------------------------------------
# Déclaration des fonctions
# ----------------------------------------------------------------------------
# fonction petale(rayon,orientaion) qui trace un pétale :
def petale(rayon,orientaion):
setheading(orientaion)
"""
code à compléter
"""
# fonction rosace(R,c1,c2,c3) qui trace une rosace en appelant plusieurs fois la fonction petale() :
def rosace(R,c1,c2,c3):
color(c1)
circle(R)
angle=60
for i in range(6)
color(c2,c3)
petale(R,angle)
angle=angle+60
"""
code à compléter
"""
# ----------------------------------------------------------------------------
# Programme principal
# ----------------------------------------------------------------------------
# configure la taille de la fenêtre :
setup(800,800)
# donne un titre à la fenêtre pour la signer :
title('2025/2026 : rosace version 3')
# efface le curseur de la tortue :
hideturtle()
# trace en vitesse rapide :
speed(0)
# déplace le curseur avant de tracer la prochaine rosace :
up()
goto(0,-300)
down()
# appelle la fonction rosace() en lui passant en paramètre le rayon et les 3 couleurs :
rosace(300,'#1F2BDF','#DDB5DF','#950A2E')
# libère la fenêtre de la tortue :
done()
Pour obtenir plusieurs sous-rosaces il faudra appeler plusieurs fois la fonction rosace(R,c1,c2,c3) dans le programme principal de rosace_v3.py.
Une fois que vous avez une rosace composée de plusieurs sous-rosaces, enregistrez votre programme rosace_v3.py puis complexifiez-le pour jouez maintenant avec les couleurs afin de colorer votre rosace complexe avec des nuances de couleurs assortis, armoniques et suffisamment contrastées pour bien identifier les différents pétales et les différentes "sous roraces". N'hésitez pas à faire plusieurs essais de couleurs.
Si besoin, on pourra passer en paramètre aux fonctions petale() et rosace() de nouvelles couleurs à utiliser (couleur du trait et couleur du fond) en plus des paramètres actuels.
N'oubliez pas d'ajouter le titre suivant à votre programme rosace_v3.py afin de signer votre création dans la barre de titre de la fenêtre de la tortue :
title('2025/2026 : rosace version 3')
Rappel : votre programme rosace_v3.py est totalement terminé si :
- il possède un titre comme indiqué ci-dessus
- il trace les rosaces en vitesse rapide : speed(0)
- le curseur de la tortue est caché : hideturtle()
- la rosace principale est centrée dans la fenêtre de la tortue qui a une taille de 800x800 : setup(800,800)
Nouvelles rosaces créées en 2025/2026 :
Les rosaces Version 2 :
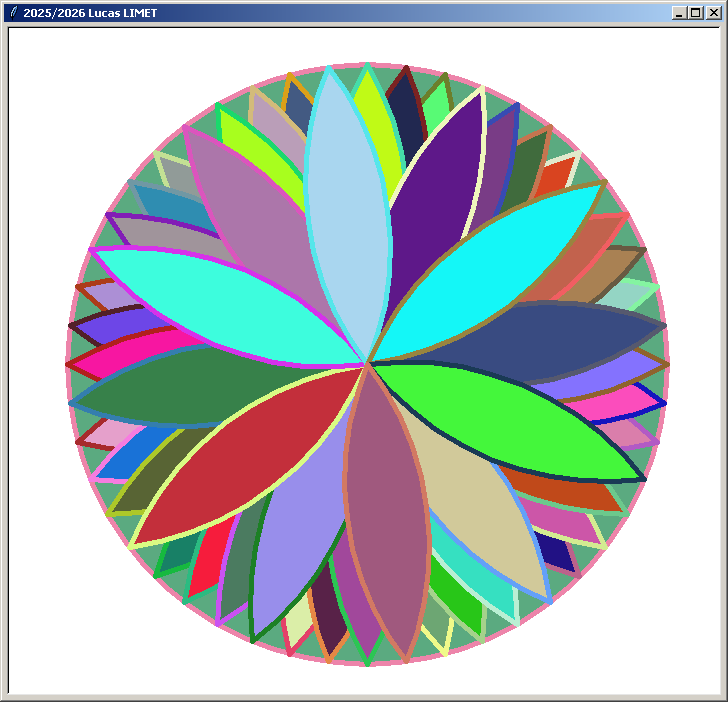
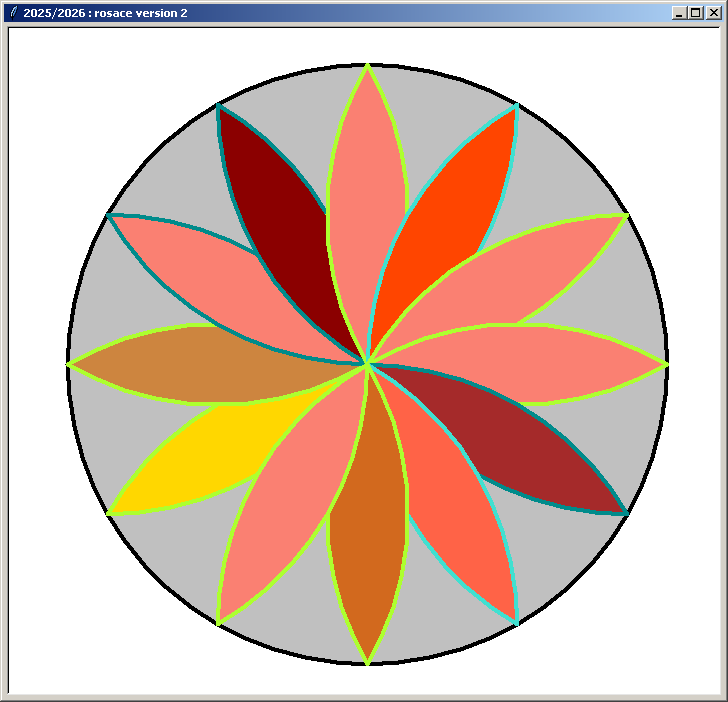
Les rosaces Version 3 :
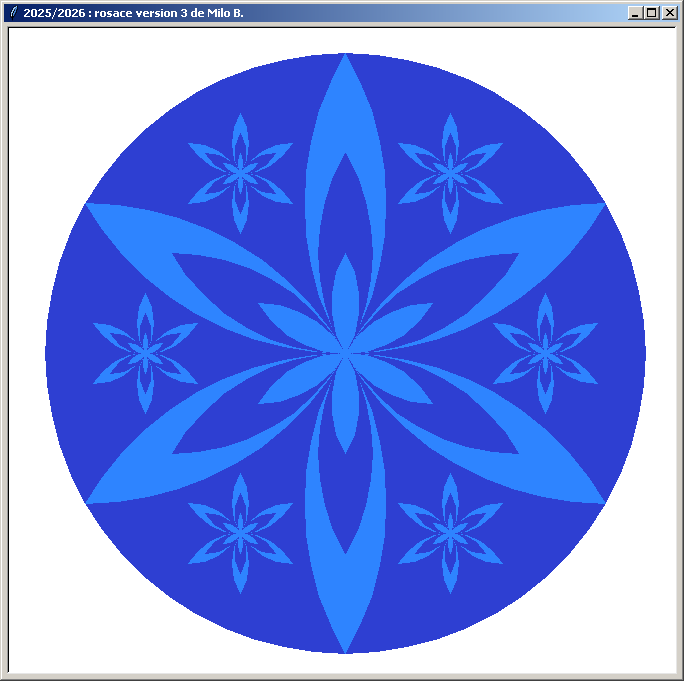




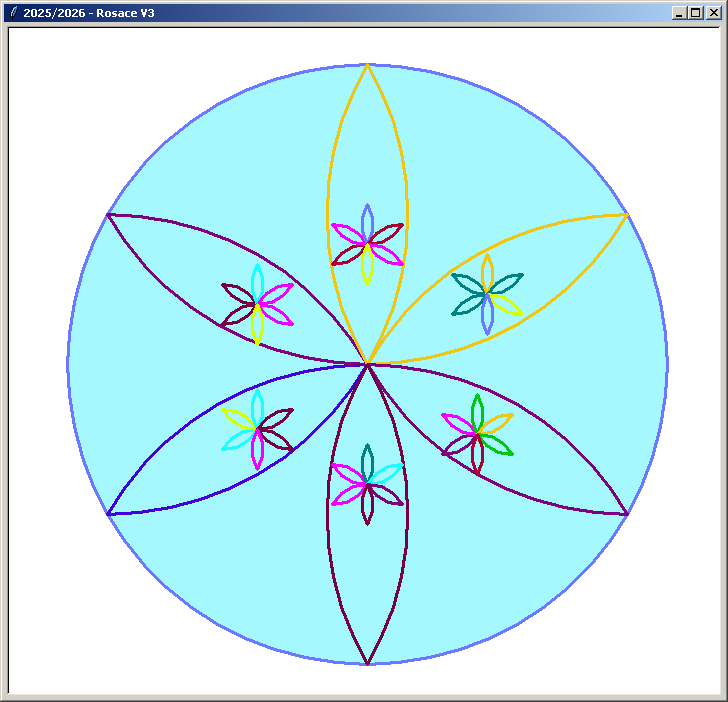
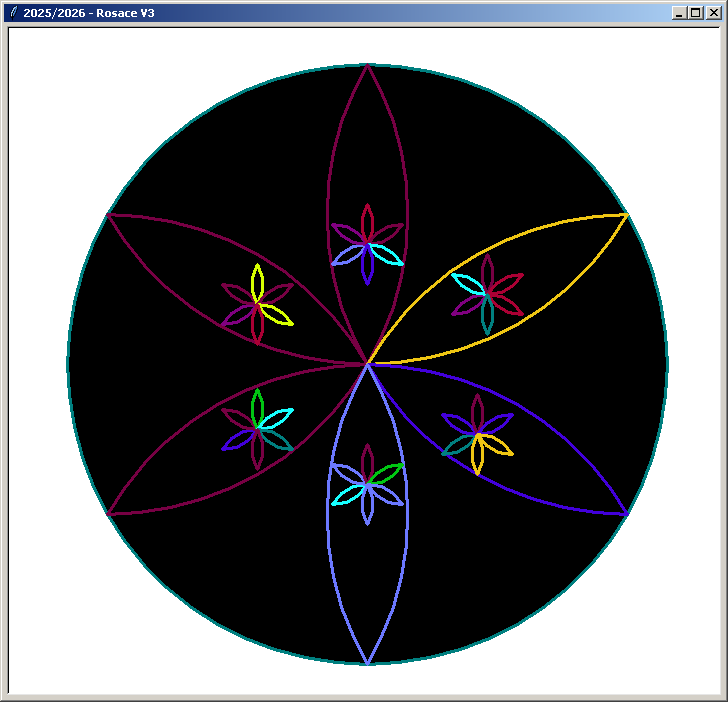
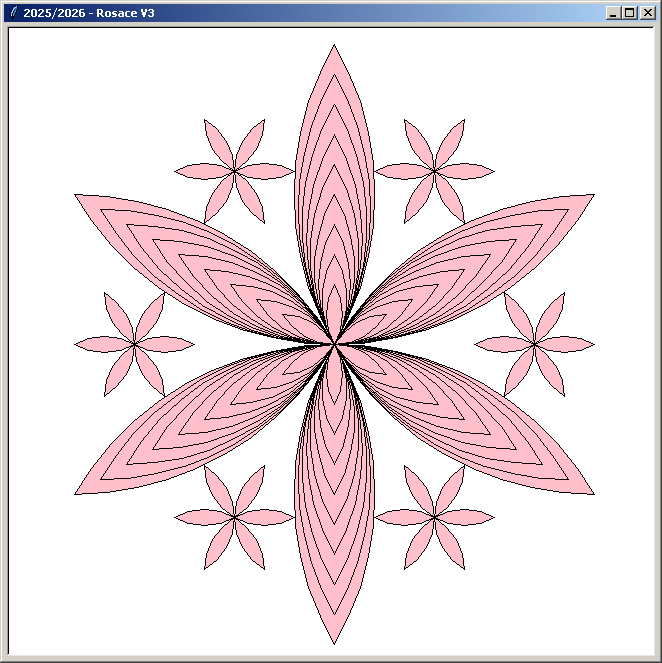




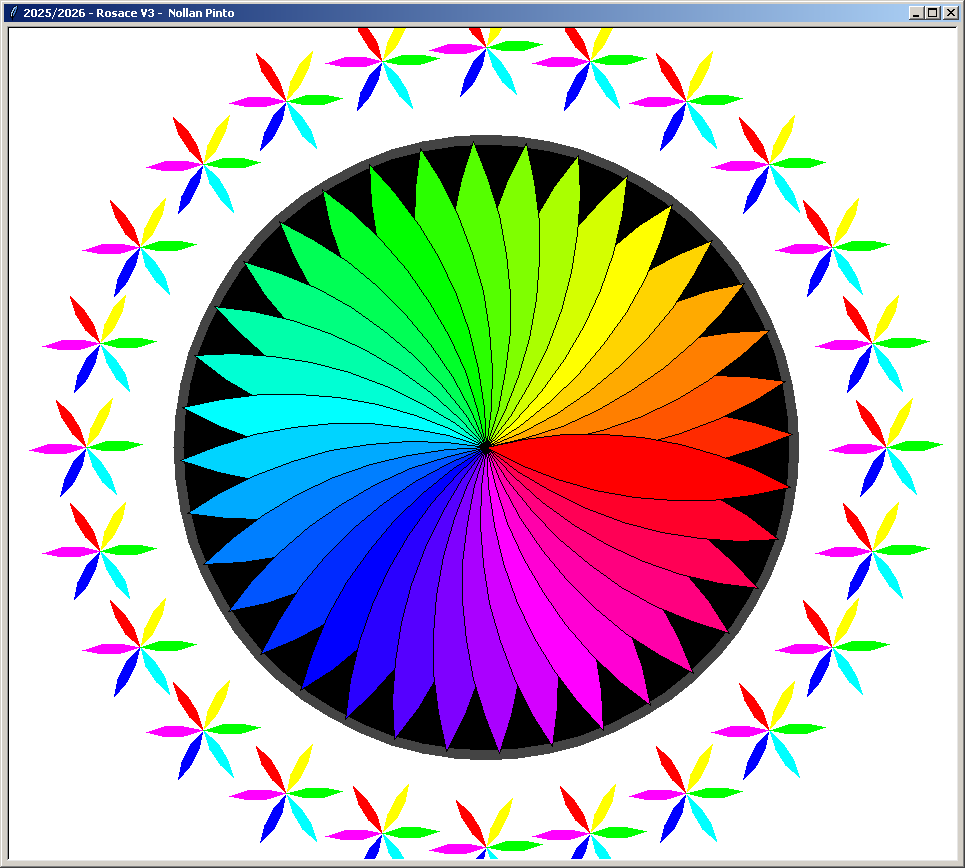
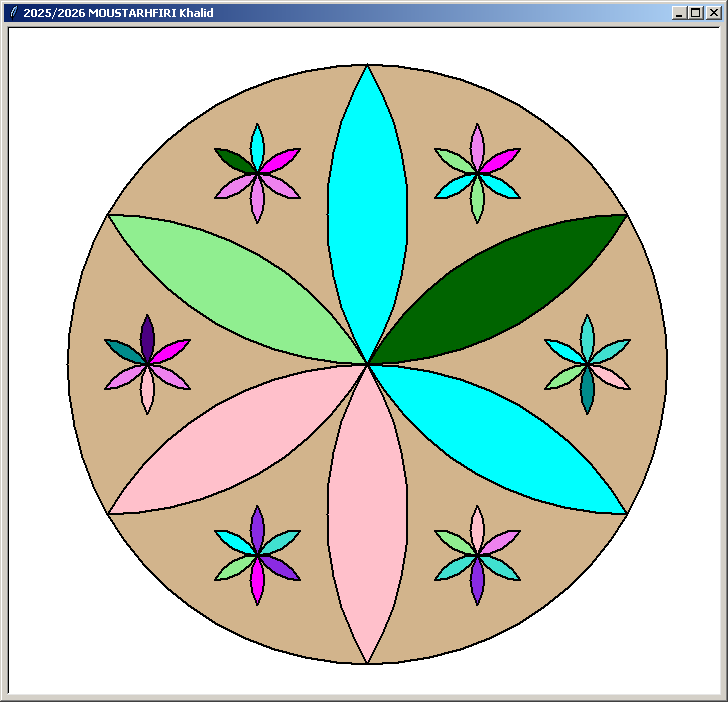












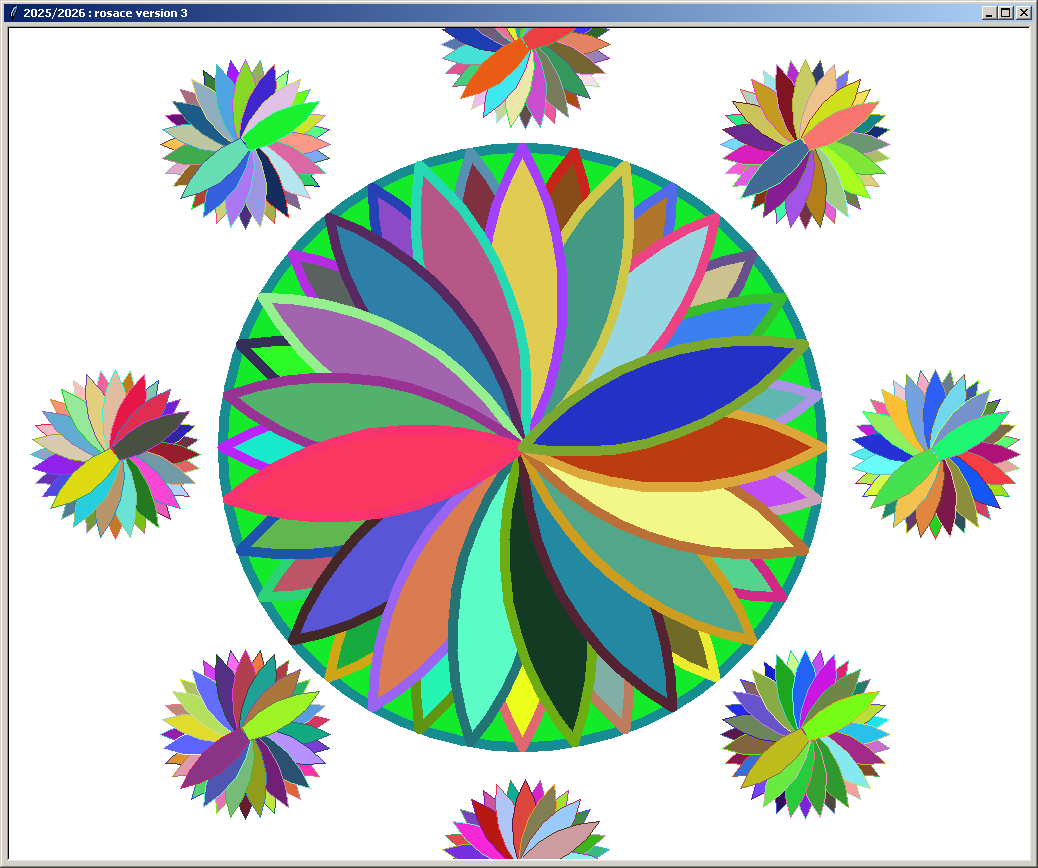

Autres compositions :
Cette figure n'est pas une rosace : c'est un ensemble de cercles et non un ensemble de pétales
Chaque fleur est une rosace
Tout un personnage entièrement dessiné à la tortue dans les moindres détails
Pour visionner toutes les rosaces créées durant les années passées cliquez ici
Pour visionner touts les sapins de Noël créées durant les années passées cliquez ici
Application 4 : les triangles imbriqués
On désire tracer avec le module Turtle de Python la figure suivante.
On part d'un triangle équilatéral de côté 600 :
En joignant chaque milieu des 3 côtés du triangle on obtient un nouveau triangle au centre :
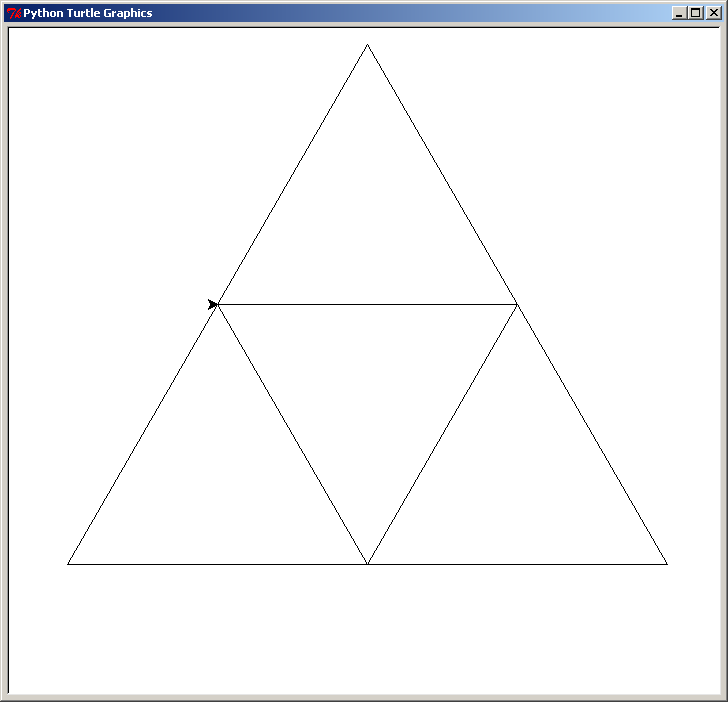
Nous avons maintenant 4 triangles : 3 triangles "à l'endroit" et 1 triangle "à l'envers" (le triangle central). Pour chacun des 3 triangles à l'endroit, toujours en joignant le milieu de leur 3 côtés, traçons 3 nouveaux triangles à l'envers.
Voici le triangle en bas à gauche :
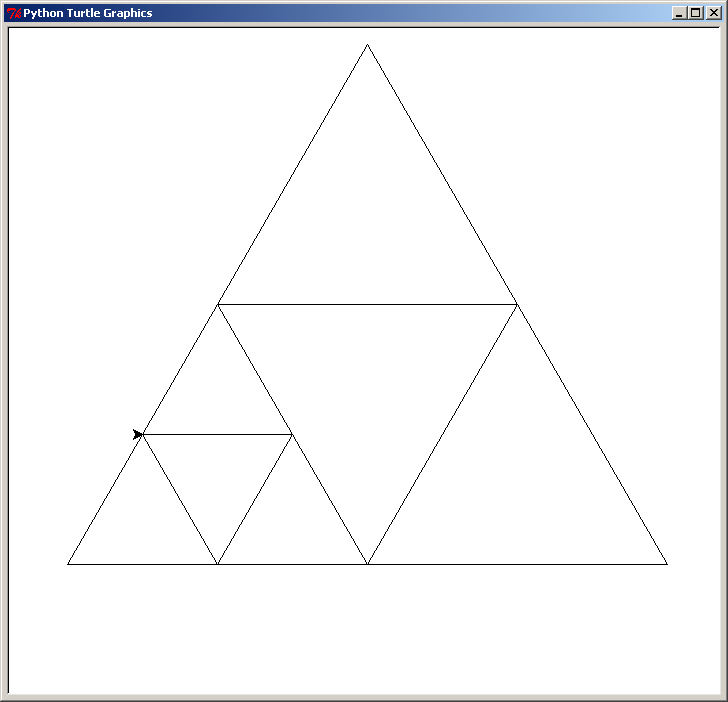
Voici le triangle en bas à droite :
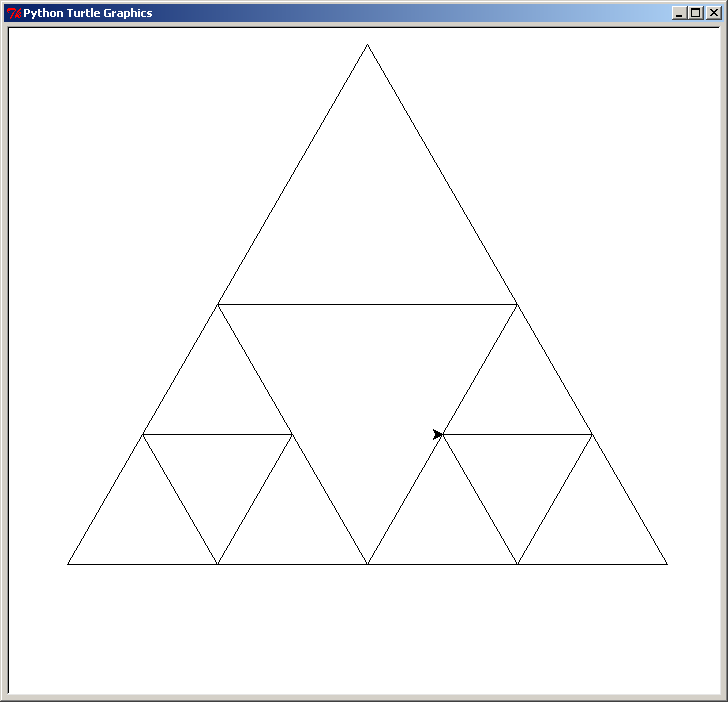
Et voici le triangle du haut :
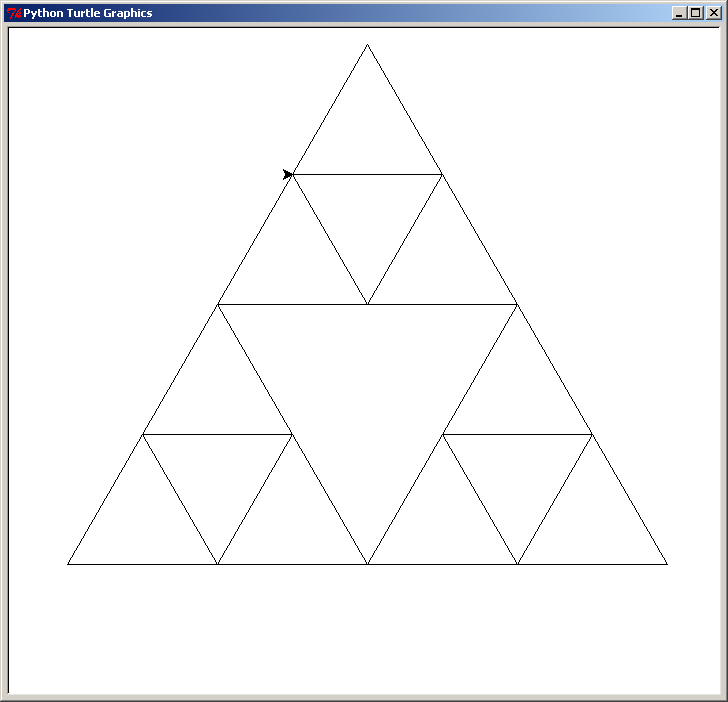
Nous avons maintenant 13 triangles : 9 triangles "à l'endroit" et 4 triangles "à l'envers".
Vous l'avez compris, dans chacun des triangles à l'endroit il faut maintenant tracer un triangle à l'envers en joignant les milieux de ses côtés, puis recommencer avec tous les nouveaux triangles à l'endroit obtenus.
Voici une figure plus avancée mais non terminée :
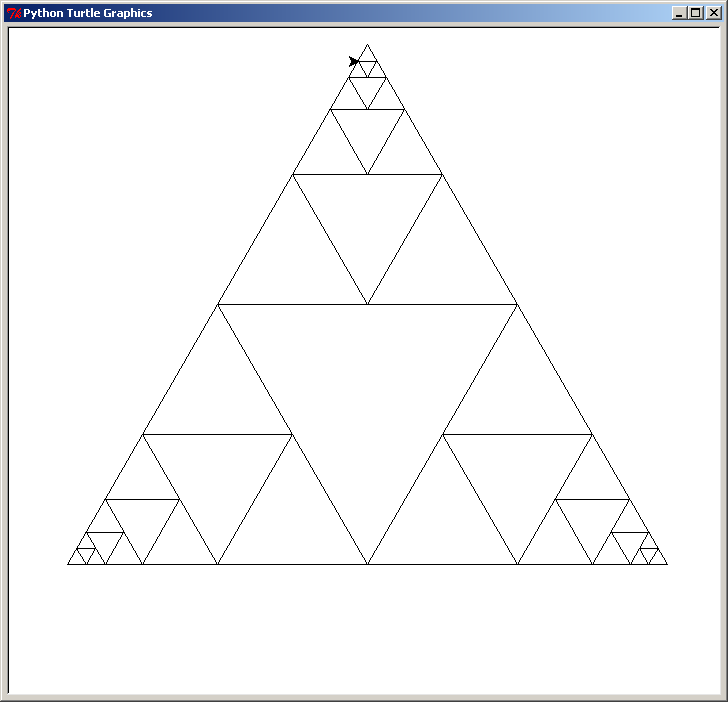
Et en voici une autre, également plus avancée mais non terminée (car il y a encore des triangles "à l'endroit" qui ne possèdent pas de triangle "à l'envers" à l'intérieur) :
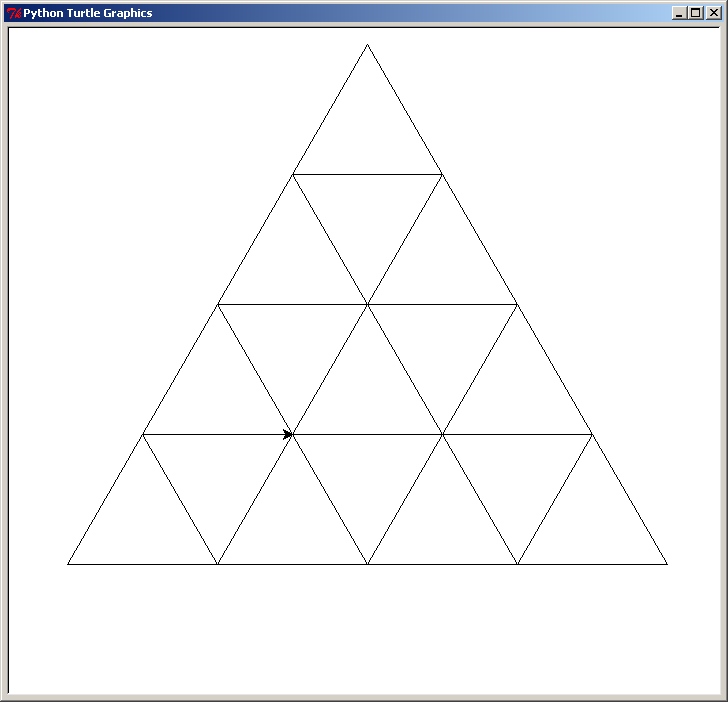
Remarques :
- il y a un seul triangle "à l'endroit" : le premier triangle de côté 600
- tous les autres triangles que l'on trace sont de triangles "à l'envers"
- tous les triangles "à l'endroit" doivent avoir en leur centre un triangle "à l'envers"
- tous les triangles "à l'envers" doivent rester vides
- on ne remplit que les trangles "à l'endroit"

Seuls les triangles "à l'envers" sont tracés à l'intérieur des triangles "à l'endroit"
Enfin, voici une construction complète où les triangles à l'envers ont été tracés dans tous les triangles à l'endroit :
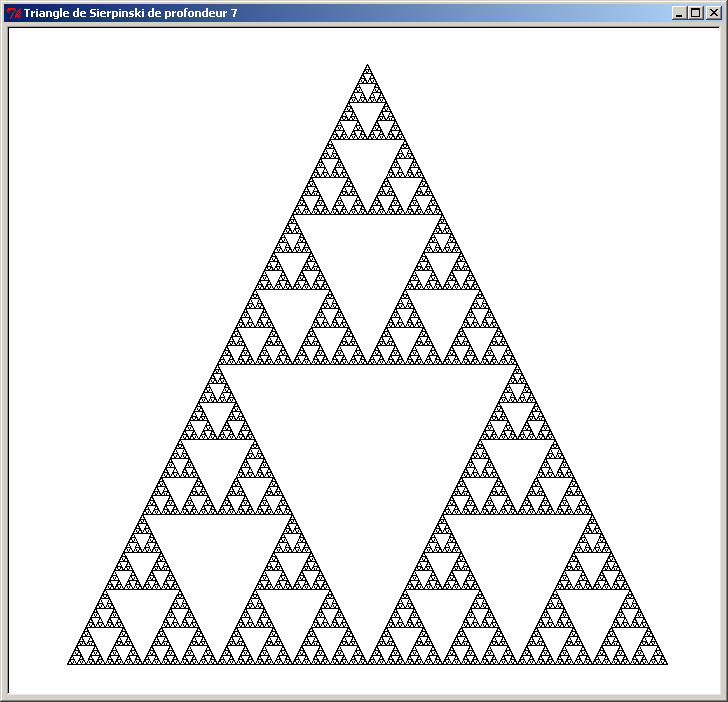
Consignes à respecter pour bien commencer :
- tous les triangles sont équilatéraux (les 3 côtés ont la même longueur et chaque angle interne vaut 60°)
- chaque triangle possède 3 côtés (3 segments de même longueur) et 3 sommets (3 points de coordonnées précises)
- le premier triangle a des côtés qui mesurent 600 (c'est le seul triangle "à l'endroit" de la figure)
- le sommet inférieur gauche du premier triangle a pour coordonnées (-300,-200)
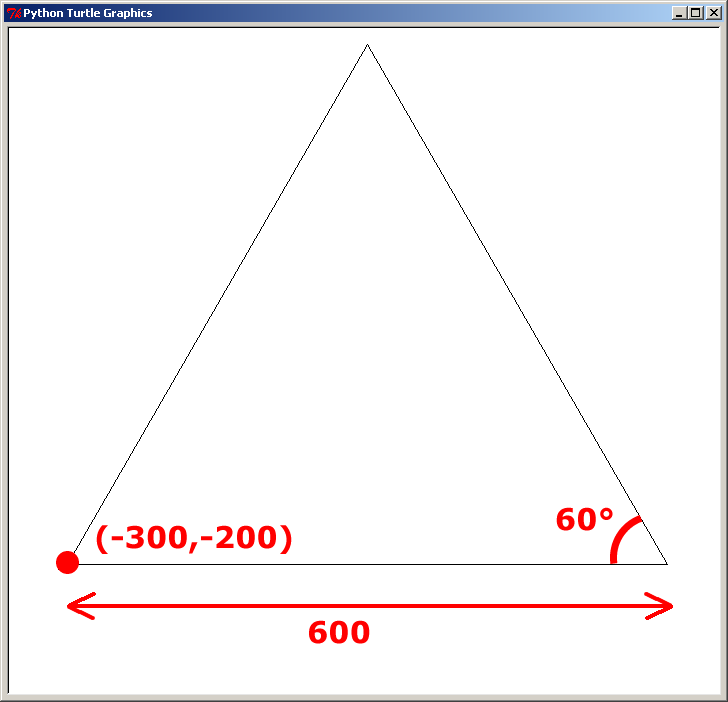
Le premier triagnle part du point (-300,-200) et a pour côté 600
Voici par exemple un programme qui trace ce premier triangle :
# les triangles imbriqués
from turtle import *
up()
goto(-300,-200)
down()
for i in range(3):
forward(600)
left(120)
done()
Il vous reste à tracer tous les autres triangles "à l'envers" internes ...
Mais afin de bien organiser le programme nous allons le découper en différentes fonctions qui seront chacune appelée en cas de besoin.
Voici le programme de base qui contient 4 fonctions utiles :
from turtle import *
#======================================================
# Déclaration des fonctions
#======================================================
# - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Trace un triangle à l'endroit et renvoi la liste de ses sommets (h : le sommet est vers le Haut)
def triangle_h(longueur):
setheading(0)
liste=[]
for i in range(3):
liste.append(position())
forward(longueur)
left(120)
return liste
# - - - - - - - - - - - - - - - - - - - - - - - - - - -
# Trace un triangle à l'envers et renvoi la liste de ses sommets (b : le sommet est vers le Bas)
def triangle_b(longueur):
setheading(0)
liste=[]
for i in range(3):
liste.append(position())
forward(longueur)
right(120)
return liste
# - - - - - - - - - - - - - - - - - - - - - - - - - - -
# déplace le curseur sans tracer :
def deplacer(xy):
up()
goto(xy[0],xy[1])
down()
# - - - - - - - - - - - - - - - - - - - - - - - - - - -
# calcule le point milieu entre deux sommets et renvoie un tuple :
def milieu(sommet1,sommet2):
x=(sommet1[0]+sommet2[0])/2
y=(sommet1[1]+sommet2[1])/2
return (x,y)
#======================================================
# Programme principal
#======================================================
# Trace le premier triangle :
segment=600
deplacer((-300,-200))
liste_sommets_1=triangle_h(segment)
# Trace le triangle du milieu :
deplacer(milieu(liste_sommets_1[0],liste_sommets_1[2]))
segment=segment/2
liste_sommets_2=triangle_b(segment)
# Il faut rajouter du code ici pour tracer les autres triangles ...
done()
Cliquez ici pour télécharger ce programme (fichier pyw)
Voici comment utiliser les fonctions ci-dessus pour tracer 3 triangles. Ce code est à ajouter juste avant le done() dans le programme principal :
segment=segment/2
deplacer(milieu(liste_sommets_2[0],liste_sommets_1[0]))
liste_sommets=triangle_b(segment)
deplacer(milieu(liste_sommets_2[0],liste_sommets_1[1]))
liste_sommets=triangle_b(segment)
deplacer(milieu(liste_sommets_2[0],liste_sommets_1[2]))
liste_sommets=triangle_b(segment)
Si on veut automatiser le tracé des triangles dans une boucle for on peut aussi utiliser un code ressemblant au suivant (à la place du bloc précédent) :
for s in range(3):
liste_sommets=liste_sommets_2
segment_1=segment
for i in range(4):
deplacer(milieu(liste_sommets[0],liste_sommets_1[s]))
segment_1=segment_1/2
liste_sommets=triangle_b(segment_1)
Mais aucune de ces solutions trace tous les triangles. Il vous reste à améliorer le programme afin de tracer le maximum de triangles "à l'envers" dans tous les triangles "à l'endroit".
Rappel : on trace uniquement les triangles à l'envers (le seul triangle à l'endroit est le premier triangle de côté 600)
Si on va très loin en dessinant des triangles de plus en plus petit on obtient alors une très belle figure fractale appelée triangle de Sierpinski :




Si tous les triangles sont "en fil de fer" voici la construction progressive du triangle de Sierpinski pour les 6 premiers niveaux :

Niveau 0 |
Niveau 1
|
Niveau 2
|
Niveau 3
|
Niveau 4
|
Niveau 5
|
Si les triangles à l'endroit sont noirs et les triangles à l'envers sont blancs voici la construction progressive du triangle de Sierpinski pour les 6 premiers niveaux :

Niveau 0 |
Niveau 1
|
Niveau 2
|
Niveau 3
|
Niveau 4
|
Niveau 5
|
Remarques sur la construction progressive du triangle de Sierpinski :
- au Niveau 0 il y a 1 triangle à l'endroit : il faut donc tracer 1 triangle à l'envers pour passer au niveau suivant
- au Niveau 1 il y a 3 triangles à l'endroit : il faut donc tracer 3 triangles à l'envers pour passer au niveau suivant
- au Niveau 2 il y a 9 triangles à l'endroit : il faut donc tracer 9 triangles à l'envers pour passer au niveau suivant
- au Niveau 3 il y a 27 triangles à l'endroit : il faut donc tracer 27 triangles à l'envers pour passer au niveau suivant
- au Niveau 4 il y a 81 triangles à l'endroit : il faut donc tracer 81 triangles à l'envers pour passer au niveau suivant
- au Niveau 5 il y a 243 triangles à l'endroit : il faut donc tracer 243 triangles à l'envers pour passer au niveau suivant
Vous l'avez compris, à chaque niveau le nombre de triangles à tracer est multiplié par 3 :
au Niveau n il y a 3n triangles à l'endroit : il faut donc tracer 3n triangles à l'envers pour passer au niveau suivant
Exemples pour les niveaux suivants :
- au Niveau 6 il y a 729 triangles à l'endroit : il faut donc tracer 729 triangles à l'envers pour passer au niveau suivant
- au Niveau 7 il y a 2 187 triangles à l'endroit : il faut donc tracer 2 187 triangles à l'envers pour passer au niveau suivant
- au Niveau 8 il y a 6 561 triangles à l'endroit : il faut donc tracer 6 561 triangles à l'envers pour passer au niveau suivant
- au Niveau 9 il y a 59 049 triangles à l'endroit : il faut donc tracer 59 049 triangles à l'envers pour passer au niveau suivant
Jusqu'au niveau 3 on peut encore tracer les triangles un par un (il y en a tout de même 27 à tracer), mais à partir du niveau 4 il faut réfléchir à une solution automatique pour tracer tous les triangles dans une boucle.
La figure obtenue est véritablement fractale à partir du niveau 5.
Et voici ce que donne le triangle de Sierpinski tracé en Python grâce au module Turtle pour les 10 premiers niveaux (de 0 à 9) :
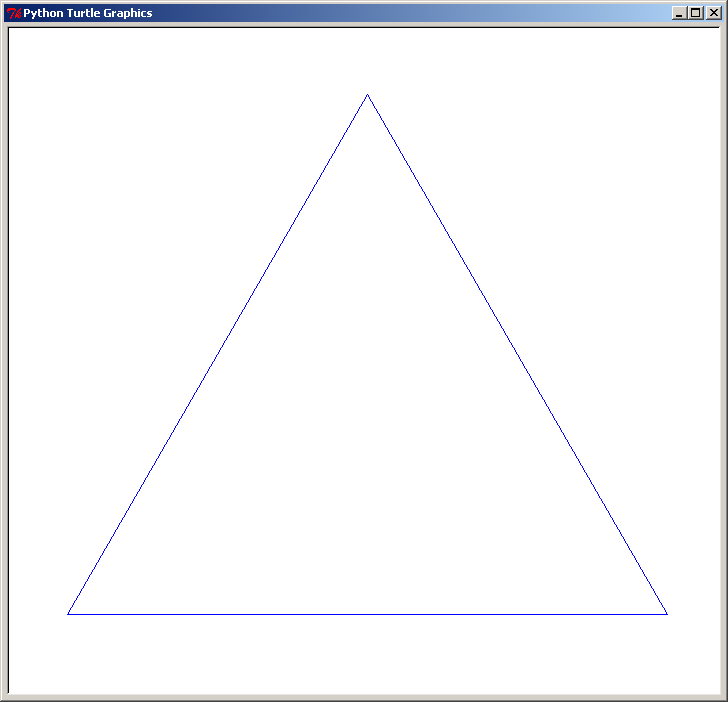
triangle de Sierpinski de niveau 0

triangle de Sierpinski de niveau 1
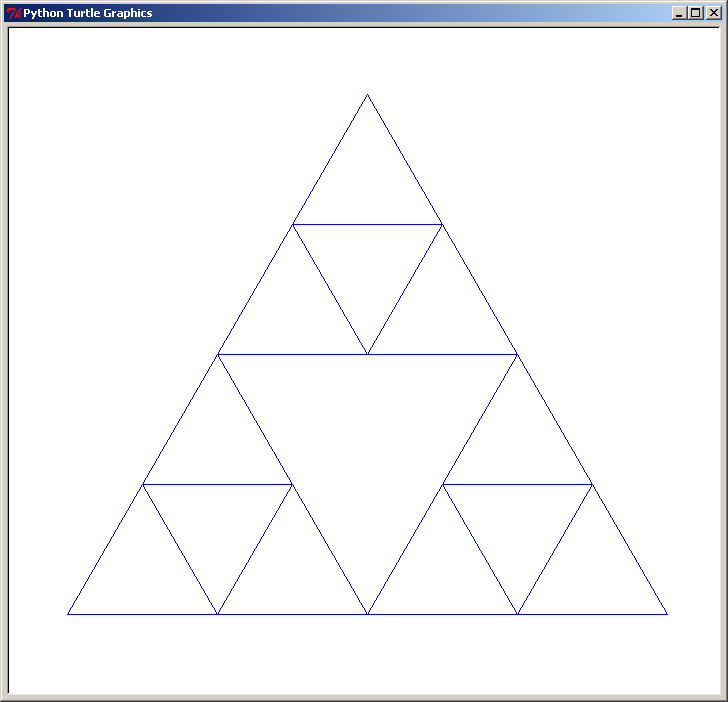
triangle de Sierpinski de niveau 2
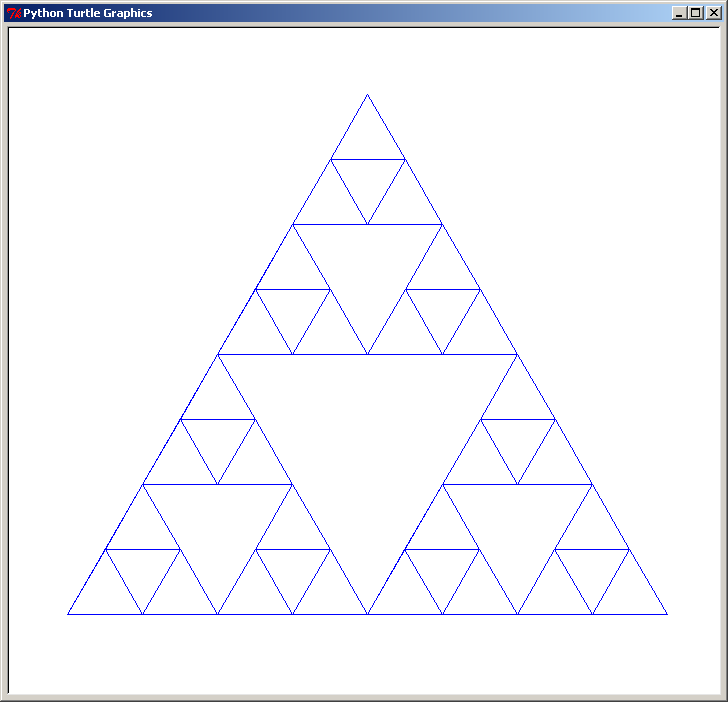
triangle de Sierpinski de niveau 3
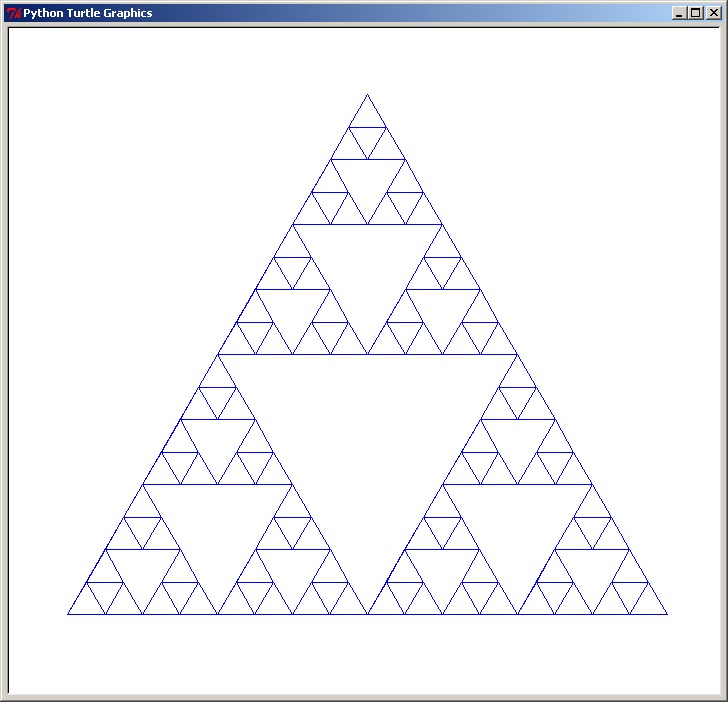
triangle de Sierpinski de niveau 4
triangle de Sierpinski de niveau 5
triangle de Sierpinski de niveau 6

triangle de Sierpinski de niveau 7

triangle de Sierpinski de niveau 8
triangle de Sierpinski de niveau 9
Cliquez ici pour plus d'informations sur le triangle de Sierpinski
Application 5 : le jeu Puissance 4
Le but de cette application 5 est de programmer en Python le jeu Puissance 4 en utilisant le module Turtle pour l'interface graphique :
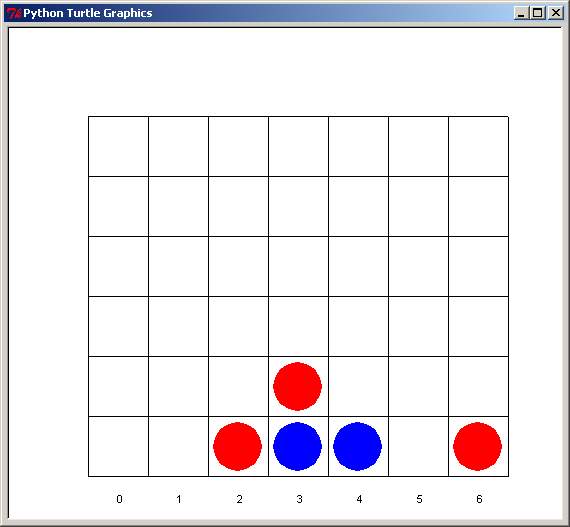
Nous commençons en un premier temps par une version très simple, que nous ferons évoluer en ajoutant progressivement des fonctionnalités en enrichissant le code source.
Chaque évolution du programme fera l'objet d'une nouvelle version du jeu.
Rappel de la règle du jeu :
Le but du jeu Puissance 4 est d'aligner une suite de 4 pions de même couleur sur une grille comptant 6 lignes et 7 colonnes. Chaque joueur dispose de 21 pions d'une couleur (ici bleu ou rouge). Tour à tour, les deux joueurs placent un pion dans la colonne de leur choix, le pion coulisse alors jusqu'à la position la plus basse possible dans la dite colonne à la suite de quoi c'est à l'adversaire de jouer.

Le vainqueur est le joueur qui réalise le premier un alignement (horizontal, vertical ou diagonal) consécutif d'au moins quatre pions de sa couleur. Si, alors que toutes les cases de la grille de jeu sont remplies, aucun des deux joueurs n'a réalisé un tel alignement, la partie est déclarée nulle.
Programme Puissance 4 version 1 :
Dans cette version totalement manuelle il n'y a pas de détection automatique des pions alignés (comme avec le jeu de société, il appartient aux joueurs d'observer la grille). Le joueur rouge commence.
Travail demandé :
Étape 1 : créez une fonction dessiner_grille() qui dessine la grille avec 7 colonnes et 6 lignes dans la fenêtre de la tortue. Les colonne seront numérotées de 0 à 6.
Étape 2 : créez une fonction dessiner_pion(x,y,couleur) qui dessine un pion dans la case (x,y) et qui attend 3 paramètres :
- le premier paramètre x correspond à la colonne : nombre entier entre 0 et 6, 0 pour la colonne de gauche
- le deuxième paramètre y correspond à la ligne : nombre entier entre 0 et 5, 0 pour la ligne du bas
- le troisième paramètre couleur correspond à la couleur du pion : 1 pour ROUGE et 2 pour BLEU
Par exemple si on appelle la fonction dessiner_pion(4,0,2) elle doit dessiner un pion bleu dans la case (4,0) : colonne 4 ligne 0.
Étape 3 : écrire le programme principal qui demande à tour de rôle aux joueurs la colonne où ils veulent jouer. Le programme doit gérer la ligne et le nombre de pions présent dans chaque colonne en le mémorisant dans une liste liste_colonne qui vaut [0,0,0,0,0,0,0] au démarrage lorsque la grille est vide.
Étape 4 : améliorez votre programme Puissance 4 afin qu'il détecte lorsque la grille est pleine (42 pions joués) et qu'il affiche alors le message "Grille pleine"
Dans cette version 1 il y a 2 joueurs humains qui jouent à tour de rôle en saisissant au clavier le numéro de la colonne choisie (entre 0 et 6).
Solution de la version 1 :
Voici une solution commentée pour cette version 1 de Puissance 4 à tester dans EduPython : puissance_4_v1.pyw
Évidemment cette solution n'est pas unique, mais elle répond aux 4 étapes demandées dans la version 1.
Dans ce programme la variable grille est une liste à 2 dimensions représentant l'état de la grille (0 : case vide, 1 : pion ROUGE ou 2 : pion BLEU)
Au départ la liste grille contient seulement des 0 puisque la grille est vide :
>>> grille=[7*[0], 7*[0], 7*[0], 7*[0], 7*[0], 7*[0]]
>>> grille
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0]]
grille[5] est une liste à 7 éléments représentant la ligne du bas (ligne 0) :
>>> grille[5]
[0, 0, 0, 0, 0, 0, 0]
grille[5][0] est un entier valant 0, 1 ou 2 et représente la première case de la ligne du bas :
>>> grille[5][0]
0
En modifiant grille[5][0] on modifie l'état de la case. Par exemple pour mettre un pion BLEU dans la case en bas à gauche on affecte la valeur 2 à grille[5][0] :
>>> grille[5][0]=2
>>> grille[5]
[2, 0, 0, 0, 0, 0, 0]
>>> grille
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[2, 0, 0, 0, 0, 0, 0]]
Comme vous l'aurez compris les autres cases de cette ligne sont indexées grille[5][1], grille[5][2], grille[5][3], grille[5][4], grille[5][5] et grille[5][6].
Et de la même manière pour les autres lignes :
- grille[4] est une liste à 7 éléments représentant la 2ème ligne en partant du bas (ligne 1)
- grille[3] est une liste à 7 éléments représentant la 3ème ligne en partant du bas (ligne 2)
- grille[2] est une liste à 7 éléments représentant la 4ème ligne en partant du bas (ligne 3)
- grille[1] est une liste à 7 éléments représentant la 5ème ligne en partant du bas (ligne 4)
- grille[0] est une liste à 7 éléments représentant la 6ème ligne en partant du bas, c'est-à-dire la ligne du haut de la grille (ligne 5)
Chaque fois qu'on joue un nouveau pion le programme puissance_4_v1.pyw affiche sur la sortie standard l'état de la variable grille afin d'observer l'évolution de cette double liste.
Libre à chacun de tester cette version 1 dans EduPython, de s'en inspirer pour améliorer votre programme, ou de la prendre comme version de base à amélirer pour obtenir la version 2.
Programme Puissance 4 version 2 :
Nous allons faire évoluer la version 1 du programme Puissance 4 en ajoutant de l'interactivité : plutôt que de saisir à la main le numéro de la colonne où on veut jouer (nombre entre 0 et 6), on va faire en sorte que l'utilisateur clique simplement dans la colonne voulue avec le bouton gauche de la souris. Nous ajouterons ensuite quelques raccourcis clavier pratiques.
Pour savoir comment ajouter de l'interactivité à votre programme Python consultez le paragraphe "Comment ajouter de l'interactivité au programme ?" en bas de la page DECOUVERTE du module Turtle.
Travail demandé :
Étape 1 : améliorez votre programme Puissance 4 afin que l'utilisateur clique gauche dans la colonne où il veut jouer son pion à la place de la saisie du numéro de la colonne
Étape 2 : améliorez votre programme Puissance 4 afin que l'appui sur la touche Echap du clavier permette de recommencer une partie à zéro en vidant la grille
Dans cette version 2 il y a 2 joueurs humains qui jouent à tour de rôle en se passant la souris.
Précisions au sujet des coordonnées des colonnes :
Si on clique dans la fenêtre de la tortue on est informé du point cliqué en recevant ses coordonnées (x,y) dans la fonction appelée par onscreenclick. Pour détecter une colonne nous allons analyser seulement l'intervale de l'abscisse x (peu importe la valeur de y).
En partant du programme puissance_4_v1.pyw de la version 1 donné ci-dessus, la variable x_base représente l'abscisse de la limite gauche de la grille et la variable largeur représente la largeur d'une colonne. Il en résulte que :
- si x est compris entre x_base et x_base+largeur alors on est dans la colonne 0
- si x est compris entre x_base+largeur et x_base+2*largeur alors on est dans la colonne 1
- si x est compris entre x_base+2*largeur et x_base+3*largeur alors on est dans la colonne 2
- si x est compris entre x_base+3*largeur et x_base+4*largeur alors on est dans la colonne 3
- si x est compris entre x_base+4*largeur et x_base+5*largeur alors on est dans la colonne 4
- si x est compris entre x_base+5*largeur et x_base+6*largeur alors on est dans la colonne 5
- si x est compris entre x_base+6*largeur et x_base+7*largeur alors on est dans la colonne 6
Plus que jamais, en utilisant les variables x_base et largeur la détection des colonnes restera valable même si on modifie la position ou la taille de la grille. En revanche, si on met des valeurs absolues sous forme de nombres entiers fixes pour détecter les colonnes, il faudrait tout refaire le jour où on change la taille de la grille.
Solution de la version 2 :
Voici une solution commentée pour cette version 2 de Puissance 4 à tester dans EduPython : puissance_4_v2.pyw
Évidemment cette solution n'est pas unique, mais elle répond aux 2 étapes demandées dans la version 2 en ajoutant au jeu l'intéractivité demandée.
Cette version montre comment prendre en compte les actions venant de la souris, tout en distingant les 7 colonnes de la grille.
De plus comme demandé à l'étape 2 si on appuie sur la touche Echap (de code Escape) la grille se vide et la partie recommence à zéro (en lançant la fonction recommencer()).
Vous remarquerez il n'y a pas de boucle while dans ce programme : c'est la boucle principale lancée par done() à la fin du programme qui attend les évènements et la fermeture de la fenêtre.
Pour quitter proprement le programme il faut fermer la fenêtre de la tortue en cliquant sur la croix (il n'y a pas de raccourcis clavier programmé pour la fermeture).
Programme Puissance 4 version 3 :
Nous allons faire évoluer la version 2 du programme Puissance 4 afin de détecter automatiquement l'alignement de 4 pions de même couleur. Pour cela il faut analyser le contenu de la liste à 2 dimensions grille afin d'y détecter 4 valeurs identiques consécutives (1 pour ROUGE ou 2 pour BLEU).
Travail demandé :
Étape 1 : améliorez votre programme Puissance 4 afin qu'il détecte automatiquement 4 pions de même couleur alignés horizontalement
Étape 2 : améliorez votre programme Puissance 4 afin qu'il détecte automatiquement 4 pions de même couleur alignés verticalement
Étape 3 : améliorez votre programme Puissance 4 afin qu'il détecte automatiquement 4 pions de même couleur alignés en diagonale
Pour chacune de ces 3 étapes le programme doit afficher "Fin de la partie" ainsi que le joueur gagnant (joueur ROUGE ou joueur BLEU) lorsqu'il détecte l'alignement de 4 pions ou plus.
Si la grille est pleine et qu'il n'y a pas de gagnant le programme doit indiquer "Grille pleine : aucun gagnant".
Dans cette version 3 il y a toujours 2 joueurs humains qui jouent à tour de rôle en se passant la souris.
Piste de réflexion pour détecter les pions alignés :
Toute la réflexion pour cette version 3 de Puissance 4 est concentré dans l'analyse de la variable grille afin d'y détecter 4 éléments identiques consécutifs correspondant à l'alignement de 4 pions de même couleur.
Prenons immédiatement un exemple concret pour illustrer l'analyse à faire sur la variable grille. On va analyser la grille lorsque le jeu est dans l'état suivant :
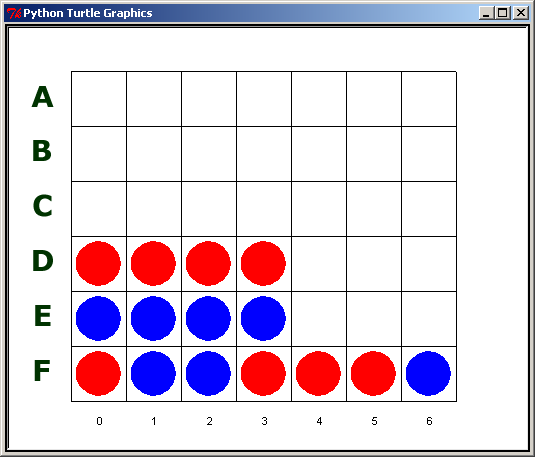
Comme illustré sur l'image ci-dessus les 6 lignes de la grille seront identifiées ici par les lettres de A (ligne du haut) à F (ligne du bas) et notre analyse portera uniquement sur la détection des pions alignés horizontalement (donc sur une même ligne).
Voici l'état de la variable grille correspondant à cet instant du jeu (0 : case vide, 1 : pion rouge, 2 : pion bleu) :
>>> grille
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 1, 0, 0, 0],
[2, 2, 2, 2, 0, 0, 0],
[1, 2, 2, 1, 1, 1, 2]]
On rappelle que grille est une liste de 6 listes, correspondant chacune à une ligne :
- la ligne A est enregistrée dans grille[0]
- la ligne B est enregistrée dans grille[1]
- la ligne C est enregistrée dans grille[2]
- la ligne D est enregistrée dans grille[3]
- la ligne E est enregistrée dans grille[4]
- la ligne F est enregistrée dans grille[5]
Les lignes A, B et C sont vides donc il y a que des zéros dans la variable grille :
>>> grille[0]
[0, 0, 0, 0, 0, 0, 0]
>>> grille[1]
[0, 0, 0, 0, 0, 0, 0]
>>> grille[2]
[0, 0, 0, 0, 0, 0, 0]
La ligne D contient 4 pions rouges alignés. Voici l'état de la ligne D dans la variable grille :
>>> grille[3]
[1, 1, 1, 1, 0, 0, 0]
La ligne E contient 4 pions bleus alignés. Voici l'état de la ligne E dans la variable grille :
>>> grille[4]
[2, 2, 2, 2, 0, 0, 0]
La ligne F contient 7 pions quelconques. Voici l'état de la ligne F dans la variable grille :
>>> grille[5]
[1, 2, 2, 1, 1, 1, 2]
Mais quelle analyse peut-on faire sur les listes grille[3], grille[4] et grille[5] ? Voici quelques exemples à affiner :
Combien de pions rouges sont présents sur la ligne D ? La méthode count liée aux listes permet de répondre à cette question :
>>> grille[3].count(1)
4
On en déduit que la ligne D contient 4 pions rouges (puisqu'il y a 4 éléments "1" dans la liste grille[3]).
Combien de case vide y'a-t-il sur la ligne D ? Là encore la méthode count y répond :
>>> grille[3].count(0)
3
On en déduit que sur la ligne D il y a 3 cases vides.
Analysons la ligne E :
>>> grille[4].count(1)
0
>>> grille[4].count(2)
4
>>> grille[4].count(0)
3
On en déduit que la ligne E contient 0 pion rouge, 4 pions bleus et 3 cases vides.
Analysons la ligne F :
>>> grille[5].count(1)
4
>>> grille[5].count(2)
3
>>> grille[5].count(0)
0
On en déduit que la ligne F contient 4 pions rouges, 3 pions bleus et 0 case vide.
Problème : la méthode count permet de compter facilement le nombre de pions d'une même couleur présent sur une ligne, mais rien n'indique si les pions sont alignés ou pas.
Dans notre exemple on sait qu'on a 4 pions rouges sur la ligne D et 4 pions rouges sur la ligne F. Or sur la ligne D les 4 pions rouges sont alignés alors que sur la ligne F ils ne sont pas alignés.
Comment distinguer les pions alignés des pions non alignés ?
Pour cela il ne suffit pas de compter le nombre de 1 présent dans la liste. Il faudrait pouvoir détecter si la sous-liste [1,1,1,1] appartient à la liste correspondant à la ligne :
- la sous-liste [1,1,1,1] appartient-elle à la liste grille[3] ? Réponse : oui, donc la ligne D contient 4 pions rouges alignés
- la sous-liste [1,1,1,1] appartient-elle à la liste grille[5] ? Réponse : non, donc la ligne F ne contient pas 4 pions rouges alignés
Le travail qu'il reste à faire est donc d'écrire une fonction capable de repérer une sous-liste dans une liste. Une fois cette fonction écrite alors il sera possible de détecter tous les alignements de pions dans la grille.
Pour alimenter votre réflexion et votre recherche expérimentale vous retrouverez toutes les fonctions et les méthodes liées aux listes dans l'unité d'apprentissage DECOUVERTE des listes sur le site python.gecif.net en plus de vos prises de notes dans votre cahier de N.S.I.
Vous l'avez compris, la maîtrise de l'analyse et de la manipulation des listes en Python est fondamentale pour trouver la solution de la version 3 de Puissance 4 et ainsi détecter l'alignement de 4 pions de même couleur : la manipulation des listes en Python n'est pas qu'une vue de l'espris mais permet de résoudre des problèmes réels.
Solution de la version 3 :
Voici une solution commentée pour cette version 3 de Puissance 4 à tester dans EduPython : puissance_4_v3.pyw
Programme Puissance 4 version 4 :
Nous allons maintenant faire évoluer le programme afin de jouer contre l'ordinateur.
Dans cette version le joueur humain aura les pions ROUGES et l'ordinateur jouera les pions BLEUS. Mais l'ordinateur ne sera pas, en un premier temps, très intelligent : il jouera au hasard une colonne non pleine parmi les 7.
Ne nous y trompons pas, même si la stratégie parait simpliste, elle peut être très déstabilisante pour un joueur humain qui chercherait à comprendre comment joue l'ordinateur ...
Travail demandé :
Étape 1 : améliorez votre programme Puissance 4 afin que les pions BLEUS soit joués automatiquement par l'ordinateur qui doit choisir au hasard une colonne non pleine
Étape 2 : améliorez votre programme Puissance 4 afin de demander au démarrage qui commence : le joueur humain (ROUGE) ou l'ordinateur (BLEU) ?
Dans cette version 4 il n'y a plus qu'un seul joueur humain, il joue les pions ROUGES à la souris, et l'ordinateur joue automatiquement les pions BLEUS.
Solution de la version 4 :
Voici une solution commentée pour cette version 4 de Puissance 4 à tester dans EduPython : puissance_4_v4.pyw
Programme Puissance 4 version 5 :
Nous allons maintenant faire évoluer la stratégie gagnante de l'ordinateur. Dans la version précédente l'ordinateur jouait au hasard dans une colonne non pleine. Ici il va essayer d'empêcher le joueur humain (ROUGE) de gagner, ou essayer lui même (BLEU) d'aligner 4 pions.
L'objectif de cette version 5 de Puissance 4 est d'analyser la structure de données grille[][] (une liste de listes) afin d'y rechercher des informations sur la répartition des pions dans la grille et de prendre en fonction des décisions pour améliorer l'intelligence artificielle mise en jeu par le programme qui joue les pions BLEUS.
Travail demandé :
Étape 1 : améliorez votre programme Puissance 4 afin que l'ordinateur empêche en priorité l'alignement de pions ROUGES :
- s'il détecte 3 pions rouges alignés il jouera en 4 ème position pour enpêcher que le joueur humain aligne 4 pions ROUGES
- sinon, s'il détecte 2 pions rouges alignés il jouera en 3 ème position pour enpêcher que le joueur humain aligne 3 pions ROUGES
- sinon il jouera au hasard dans une colonne non pleine
Étape 2 : améliorez votre programme Puissance 4 afin que l'ordinateur, s'il n'a pas de coup à casser côté ROUGE, se concentre sur l'alignement de 4 pions BLEUS plutôt que de jouer au hasard
Dans cette version 5 il y a toujours un seul joueur humain, il joue les pions ROUGES à la souris, et l'ordinateur qui joue automatiquement les pions BLEUS.
Application 6 : tracé d'un graphe
Un graphe est une figure géométrique constitué de sommets (en forme de cercle) et d'arêtes (en forme de segment de droite). Les sommets portent chacun une étiquette différentes (ici une simple lettre majuscule) :
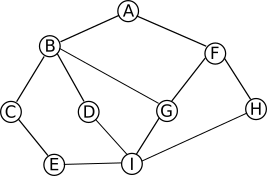
Exemple d'un graphe contenant 9 sommets
Cette application a pour but de tracer un graphe en utilisant le module Turtle de Python, et en interprétant la matrice d'adjacence écrite dans le programme.
Voici le programme de base qui doit être amélioré :
Exemples de graphes tracés avec la tortue :
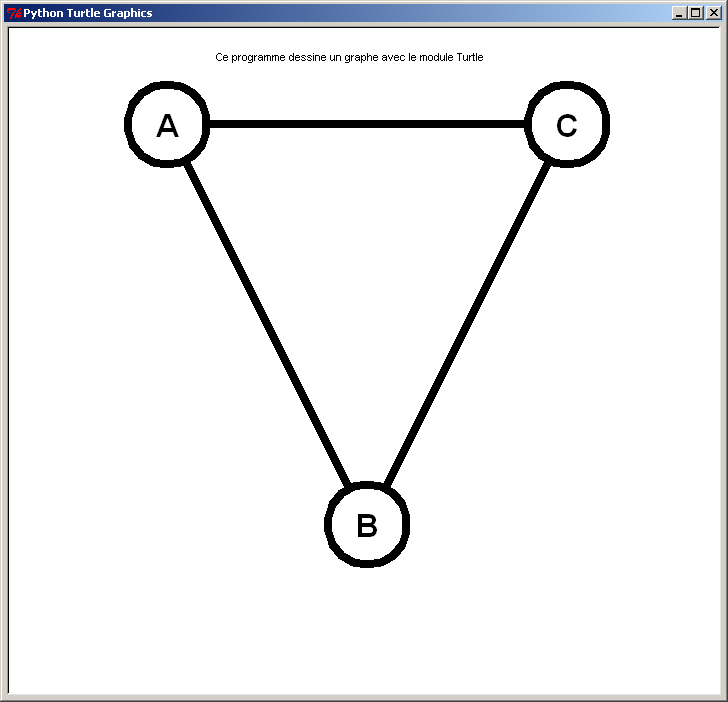
Graphe complet d'ordre 3
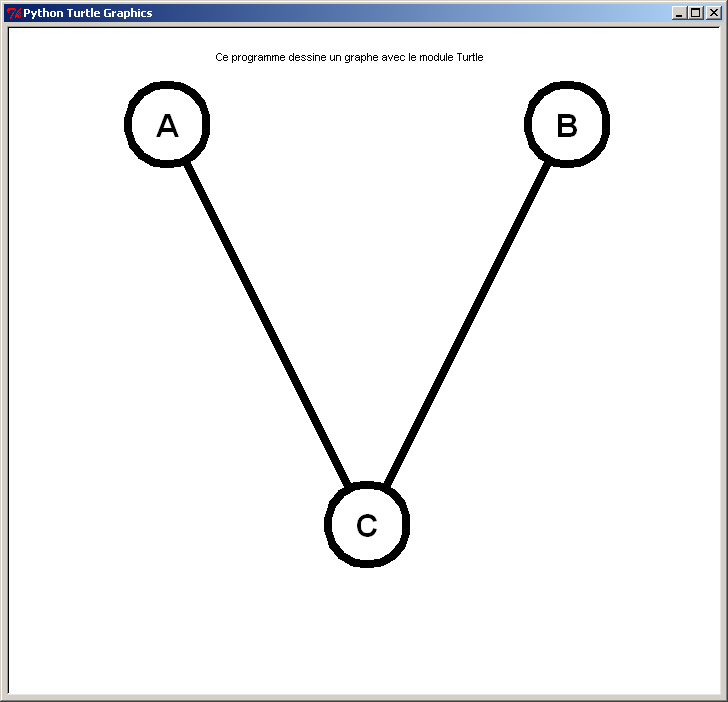
Graphe non complet d'ordre 3
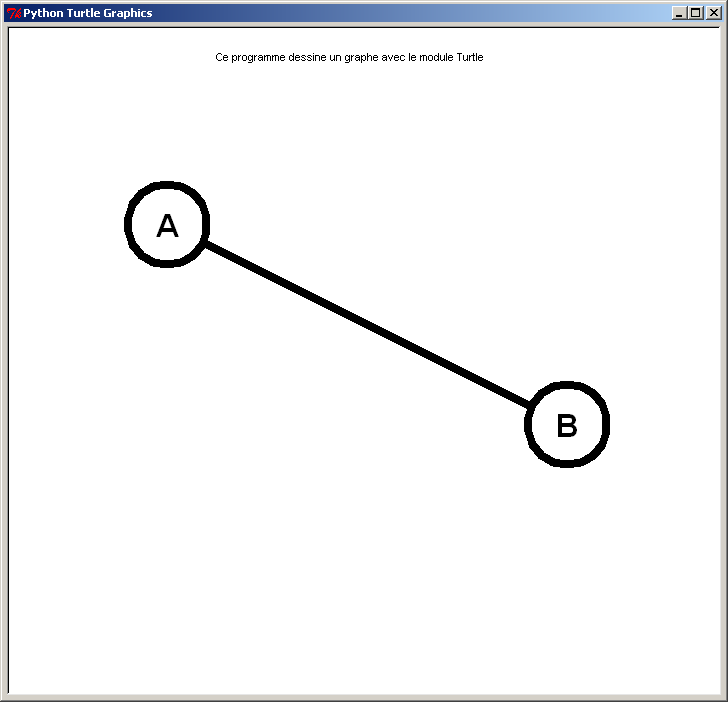
Graphe connexe d'ordre 2
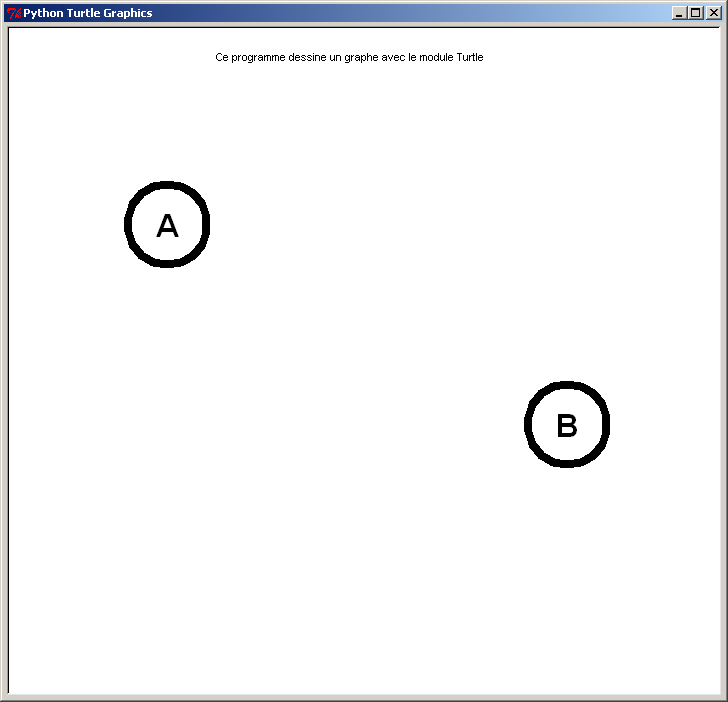
Graphe non connexe d'ordre 2
L'objectif de cette activité est d'améliorer le programme de base afin que le graphe tracé corresponde à la matrice d'adjacence : si on modifie la matrice d'adjacence et qu'on relance le programme, alors le graphe doit être modifié.
Remarques :
- la structure de données utilisée ici pour décrire la matrice d'adjacence est un dictionnaire de listes
- la structure de données utilisée ici pour décrire les coordonnées des centres des sommets est une liste de dictionnaires
- on se limitera à un graphe contenant de 2 à 9 sommets
Travail demandé :
Étape 1 : téléchargez le programme de base graphe.pyw dans votre répertoire de travail (clic droit + Enregistrer sous), testez-le dans EduPython, et améliorez-le en créant une liste de dictionnaires pour le graphe à 3 sommets afin d'inscrire une seule fois les coordonnées des centres des 3 sommets.
Étape 2 : créez la liste des coordonnées pour un graphe à 4 sommets et affichez les 4 sommets isolés (les 4 sommets doivent former un carré).
Étape 3 : améliorez votre programme afin d'afficher correctemet des éventuelles arêtes du graphe d'ordre 4 en fonction de la matrice d'adjacence.
Étape 4 : faites évoluer votre programme afin qu'il trace un graphe quelconque d'ordre 5 en fonction de la matrice d'adjacence (les 5 sommets doivent former un pendagone régulier).
Étape 5 : faites évoluer votre programme afin qu'il trace un graphe quelconque d'ordre 6 en fonction de la matrice d'adjacence (les 6 sommets doivent former un hexagone régulier).
Étape 6 : trouvez une solution afin d'automatiser le tracé des graphes d'ordre 7, 8 et 9 sans détailler tous les cas particuliers des arêtes un par un comme on a fait jusqu'à l'étape 5.
Voici quelques résultats attendus :
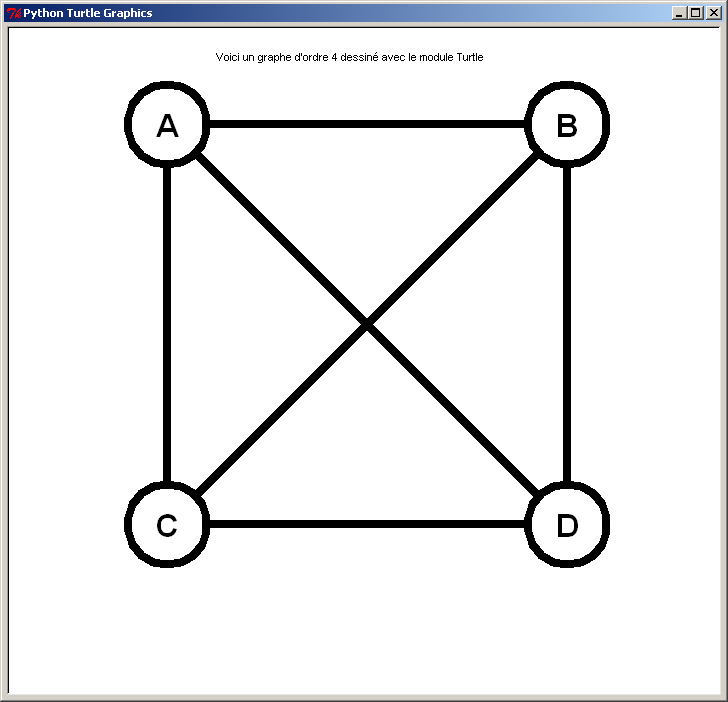
Graphe complet d'ordre 4
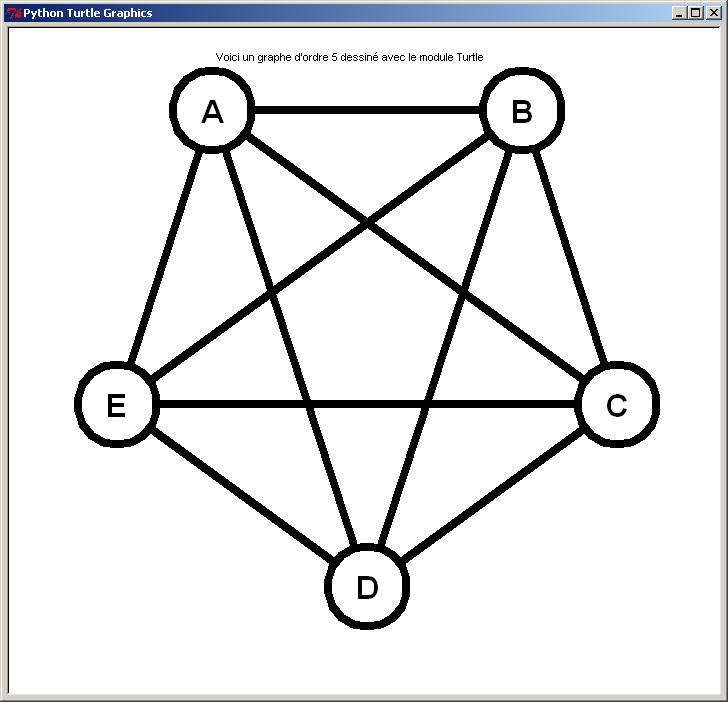
Graphe complet d'ordre 5
