Solutions des créations réalisées avec le module turtle

Voici les solutions de certaines applications afin de les comparer à vos propositions dans le but de vous auto-évaluer :

Les figures fractales

Triangle de Sierpinski : SOLUTION 1

Triangle de Sierpinski : SOLUTION 2

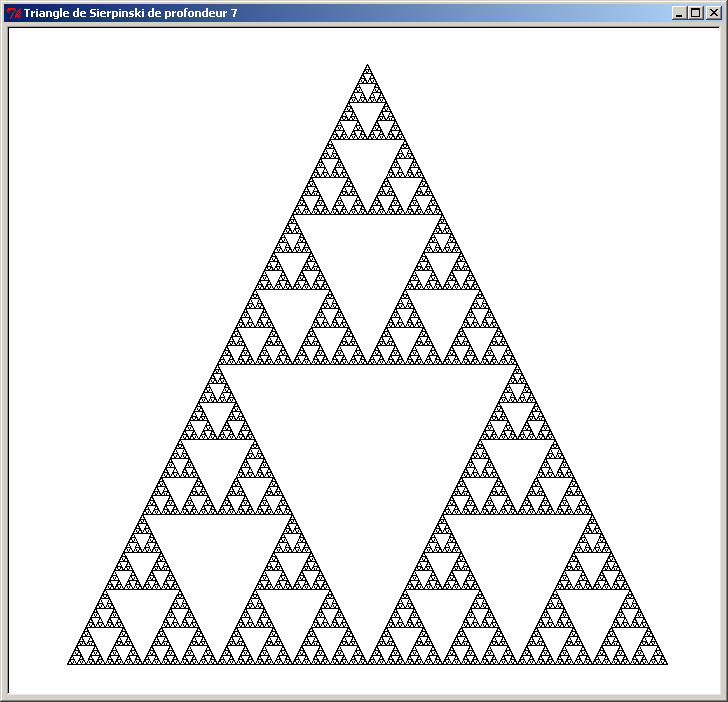
Figure fractale appelée "triangle de Sierpinski"

De la même manière on peut dessiner le "tapis de Sierpinski" où cette fois ce sont des carrés à la place des triangles :

Tapis de Sierpinski

Figure fractale appelée "tapis de Sierpinski"

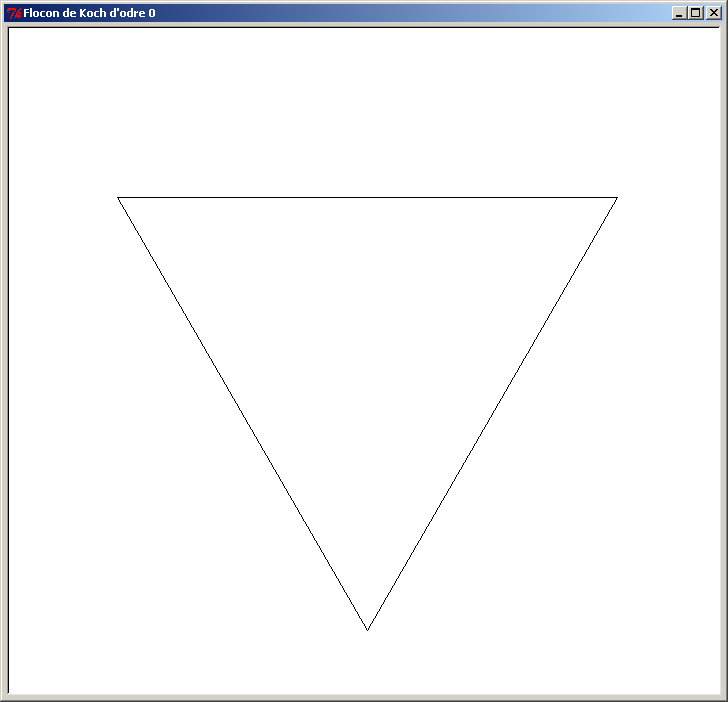
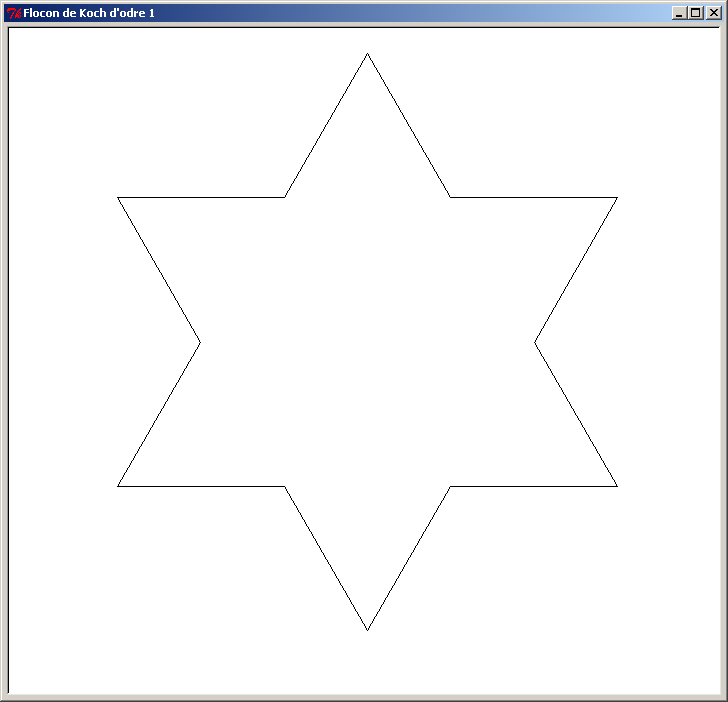
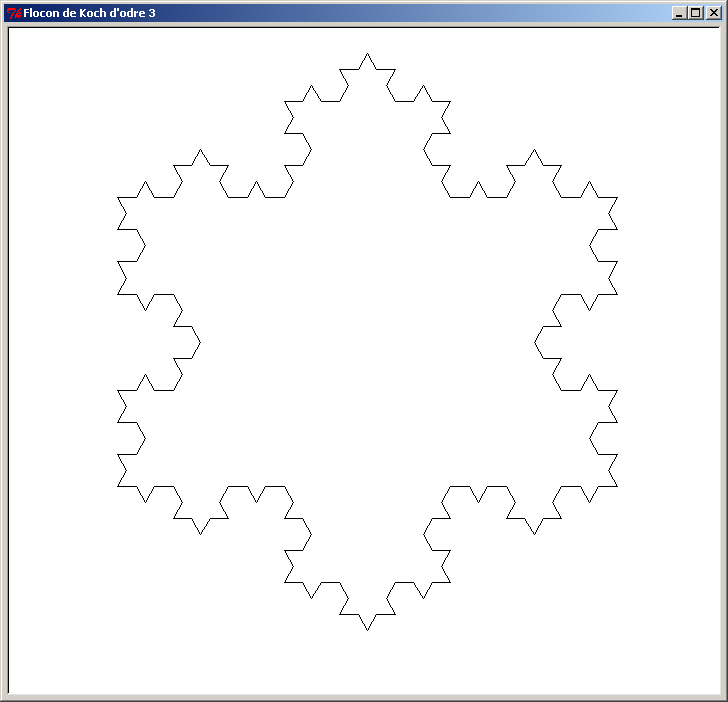
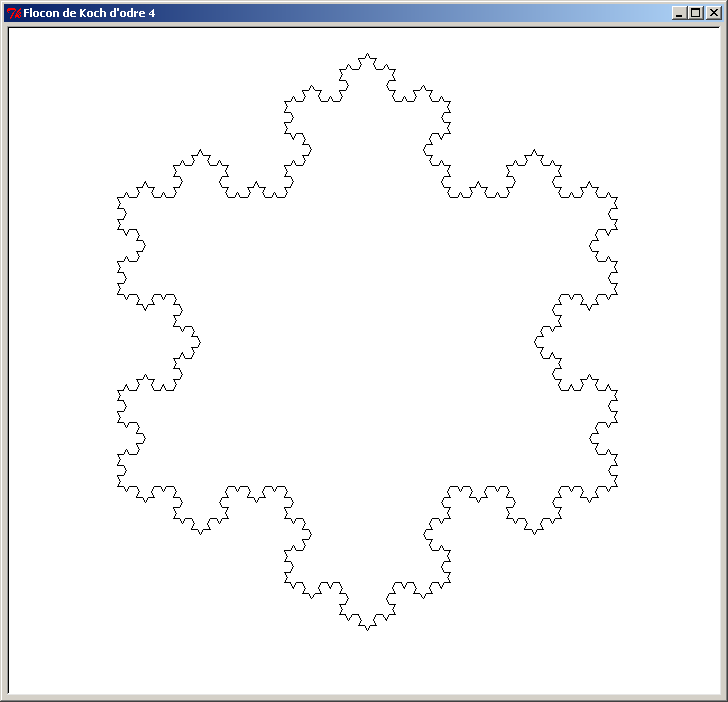
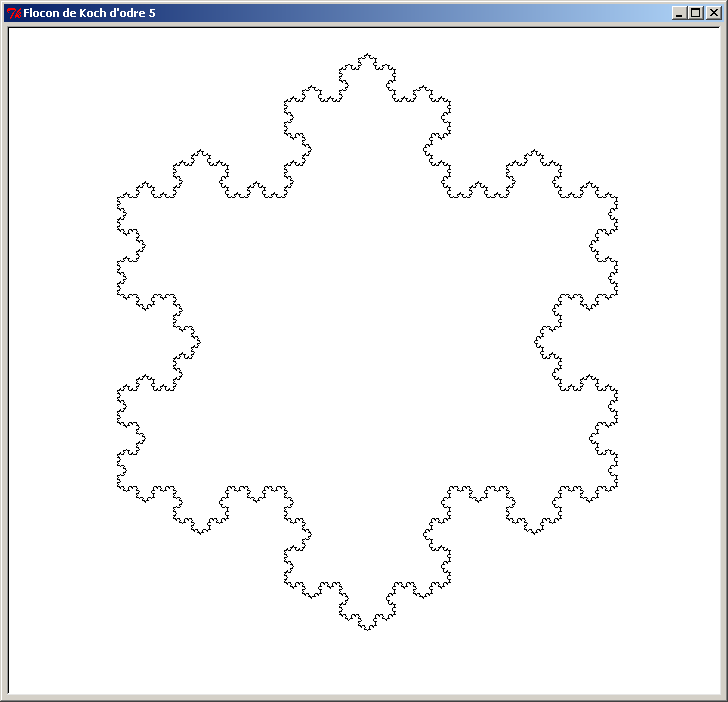
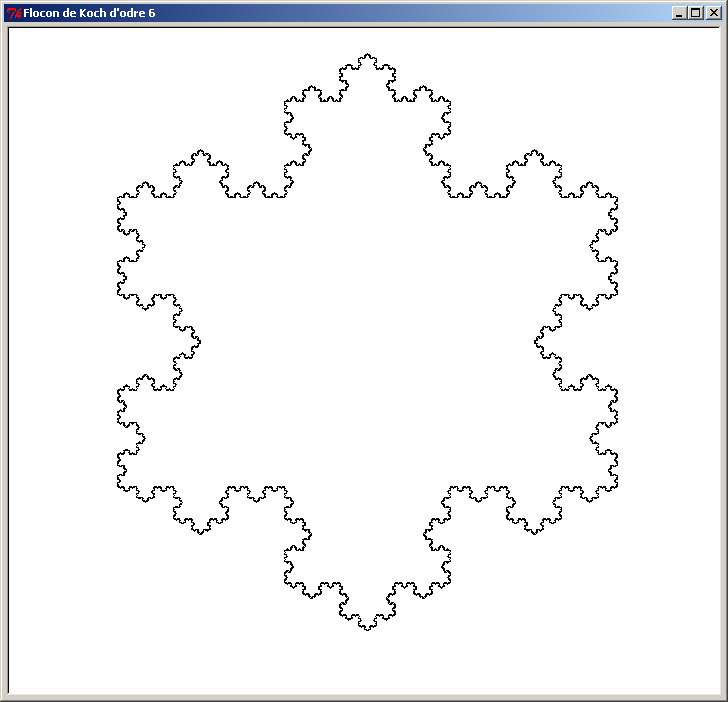
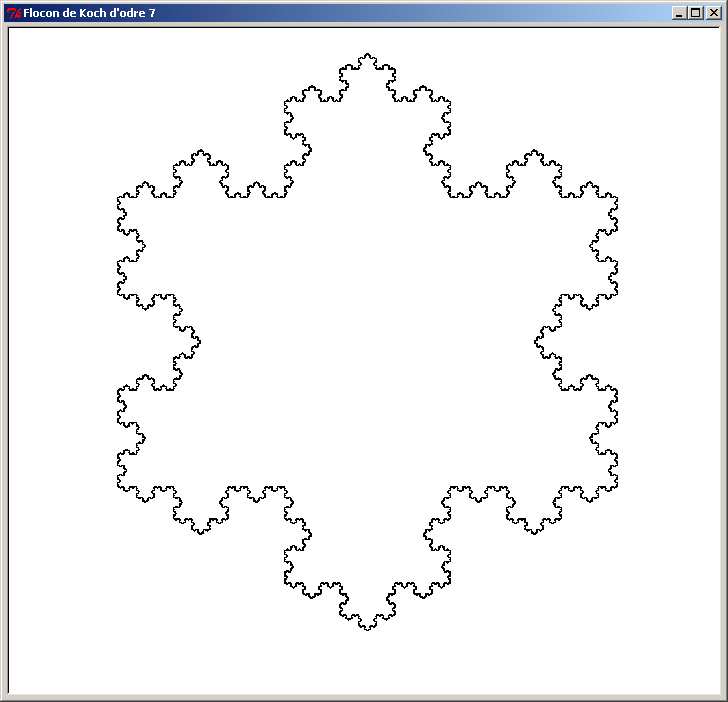
Voici une autre figure fractale appelée "Flocon de Koch". Le principe est simple : on part d'un triangle, puis on remplace chaque segment par 4 segments selon la transformation suivante :

Le segment [AB] est remplacé par 4 segments joints : [AC] [CE] [ED] et [DB]. On réitère cette transformation à chacun des nouveaux segments, et on augmente l'ordre de la figure d'une unité. Au début, la figure d'ordre 0 est un simple triangle.

Voici le Flocon de Koch pour les 8 premiers ordres (ordre 0 à ordre 7). L'ordre des figures est affiché dans le titre de la fenêtre de la tortue :

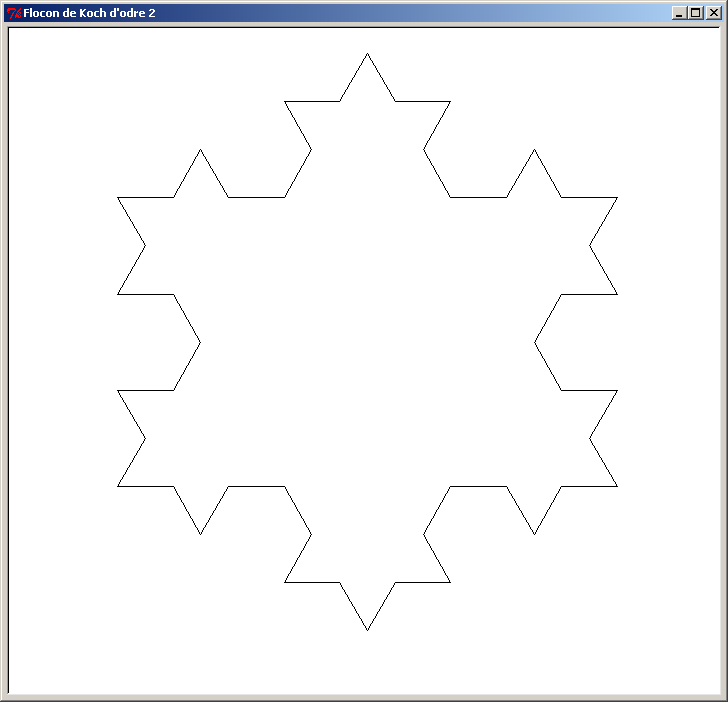
Et voici le programme en Python qui permet de tracer le flocon de Koch avec le module turtle :

Flocon de Koch

 

Les pentagones imbriqués

Voici un autre exemple de figure tracée avec le module Turtle de Pyhton. On trace un premier pentagone (5 côtés) de grande taille. On trace à l'intérieur un autre pentagone, légèrement plus petit et décalé de quelque degrés. Puis on recommence pour tracer 140 pentagones en tout. Et voici le résultat :

Les pentagones

Les 140 pentagones imbriqués

Tracé d'un graphe

Voici quelques évolutions du programme graphe.pyw de base :

graphe_v2.pyw

graphe_v3.pyw

graphe_v4.pyw

Et voici deux solutions pour tracer automatiquement un graphe complet d'ordre n :

SOLUTION 1 :

Pour tracer un graphe complet d'ordre n, on n'utilise plus de matrice d'adjacence, et on va appliquer l'algorithme suivant :

• étape 1 : on trace un polygone régulier à n côtés
• étape 2 : on récupère les coordonnées de chaque sommet du polygone dans une liste grâce à la fonction position() de la tortue
• étape 3 : on trace les arrêtes en reliant deux à deux tous les sommets, dans 2 boucles for imbriquées
• étape 4 : on dessine un rond rouge à chaque extrémité des arrêtes pour marquer les n sommets du graphe

Cette SOLUTION 1 ne fait appel à aucune connaissance mathématique pour répartir régulièrement les n sommets sur un cercle.

Voici le programme source en Python de cette SOLUTION 1 :

Graphe complet simple

Et voici les résultats obtenus (l'ordre du graphe indiqué dans le titre de la fenêtre doit être compris entre 3 et 40) :

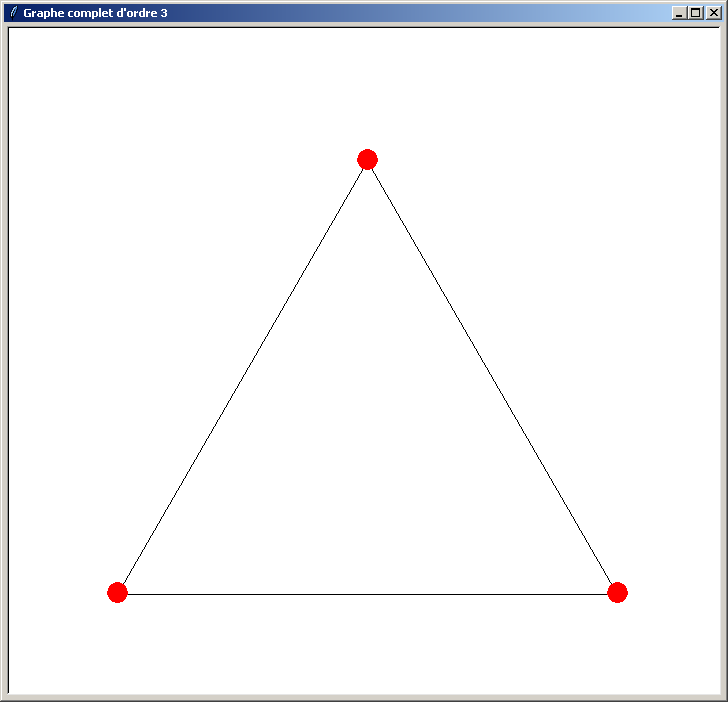
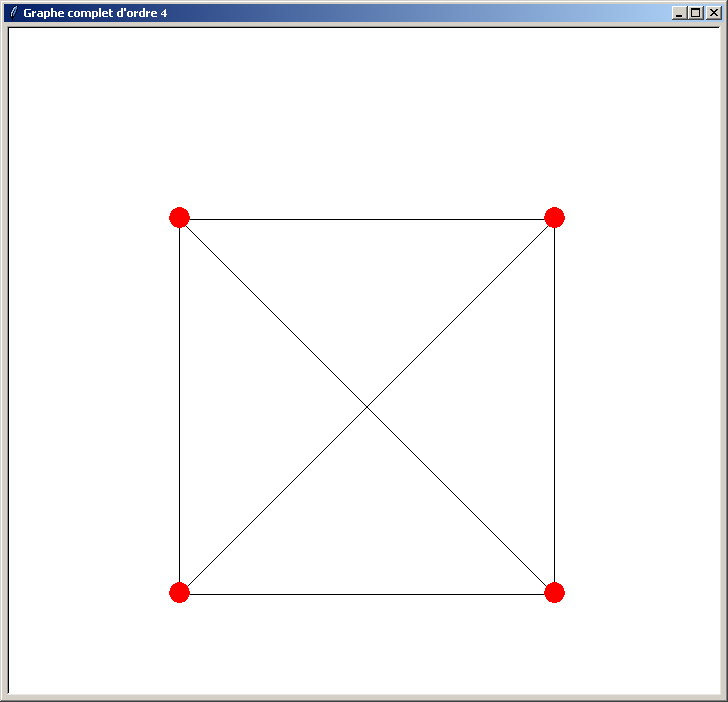
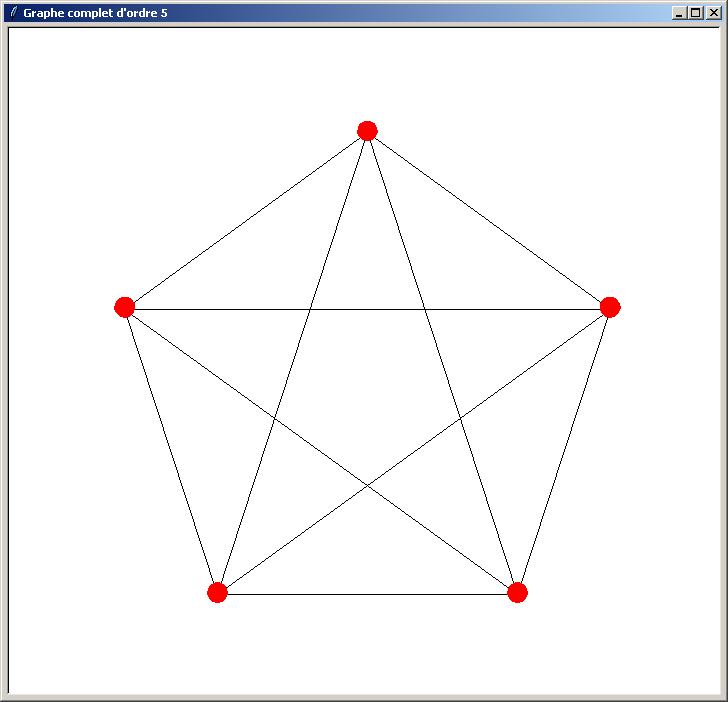
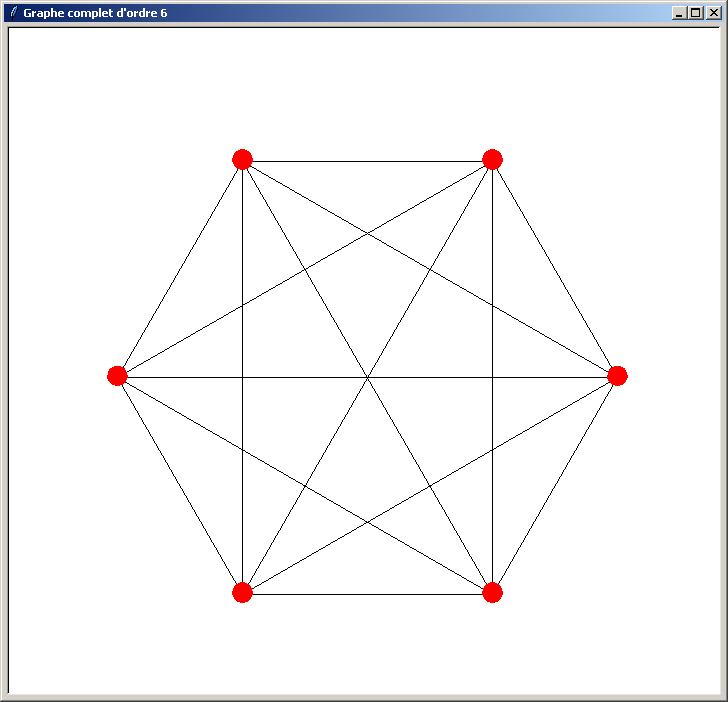
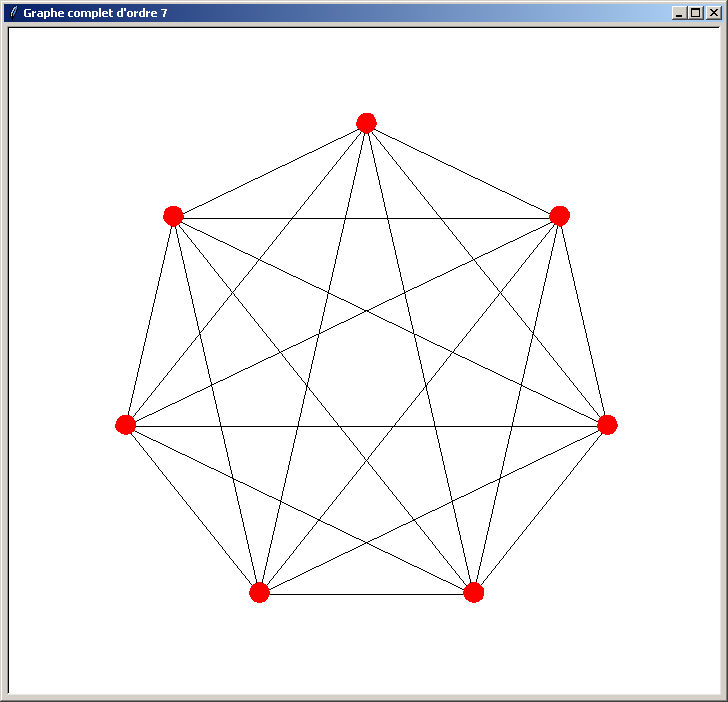
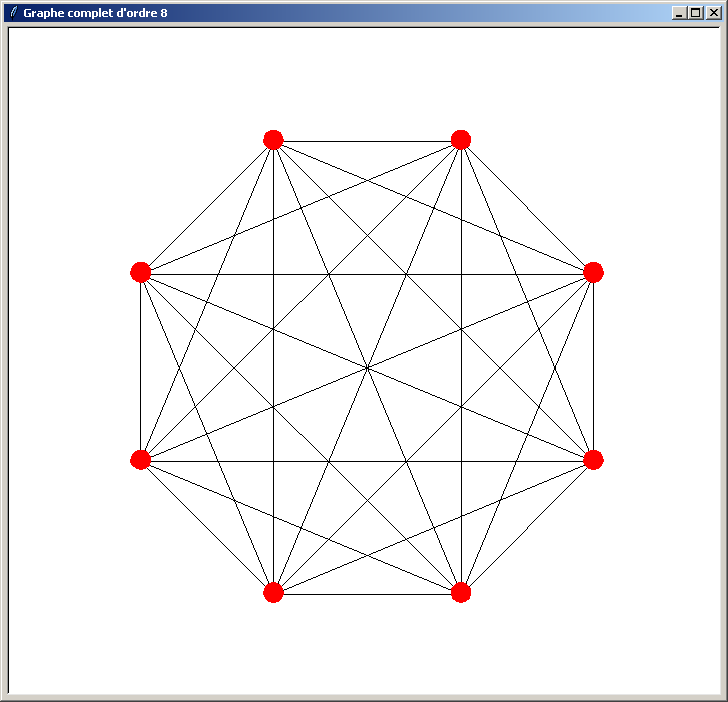
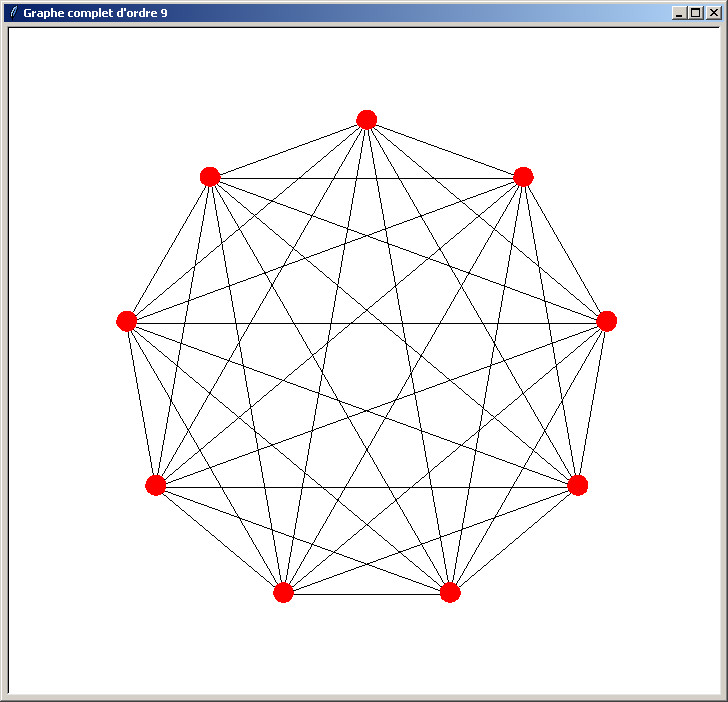
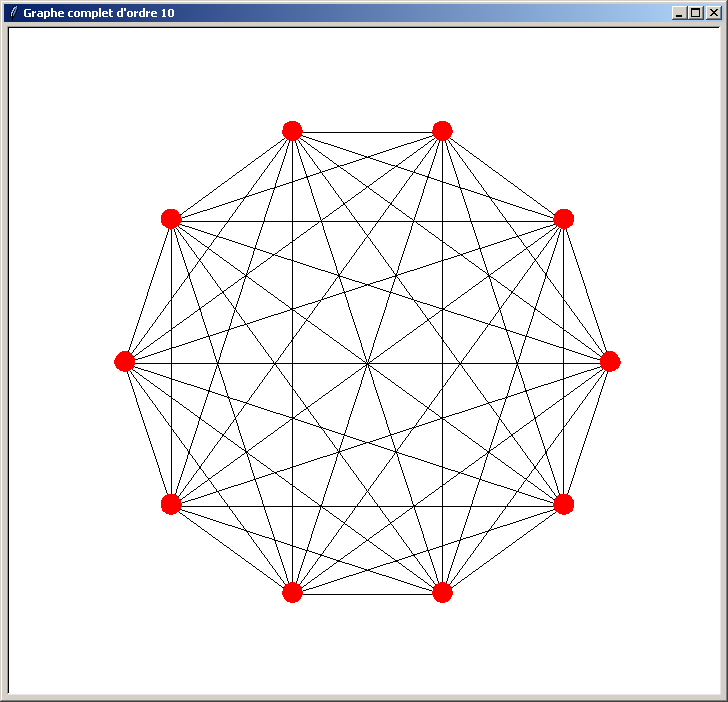
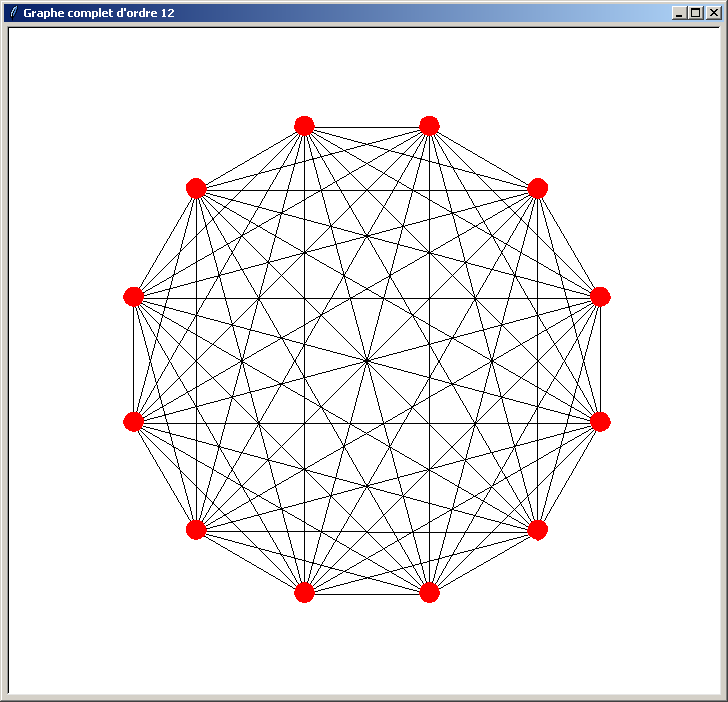
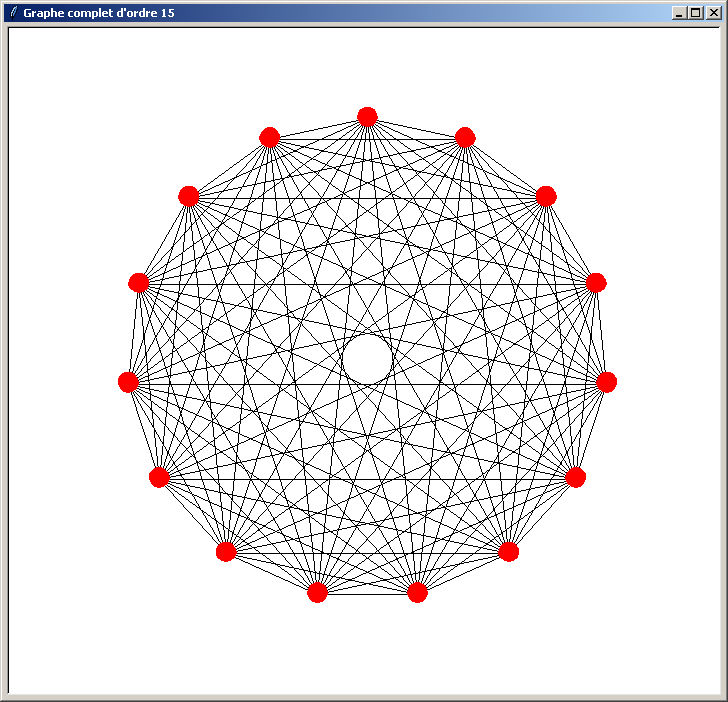
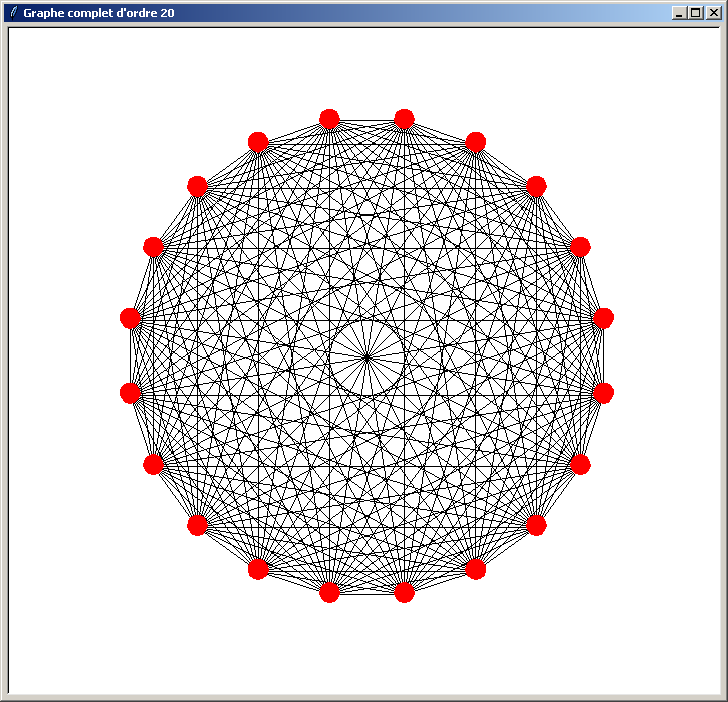
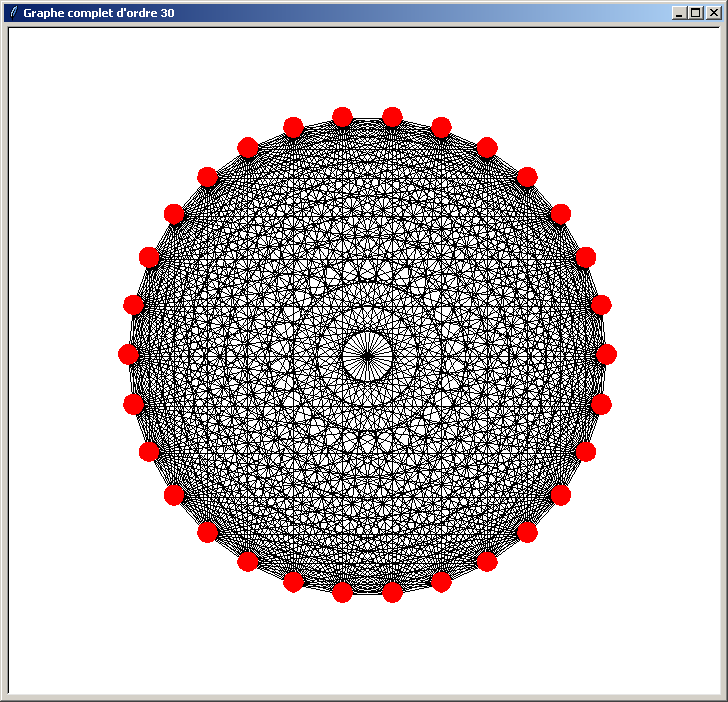
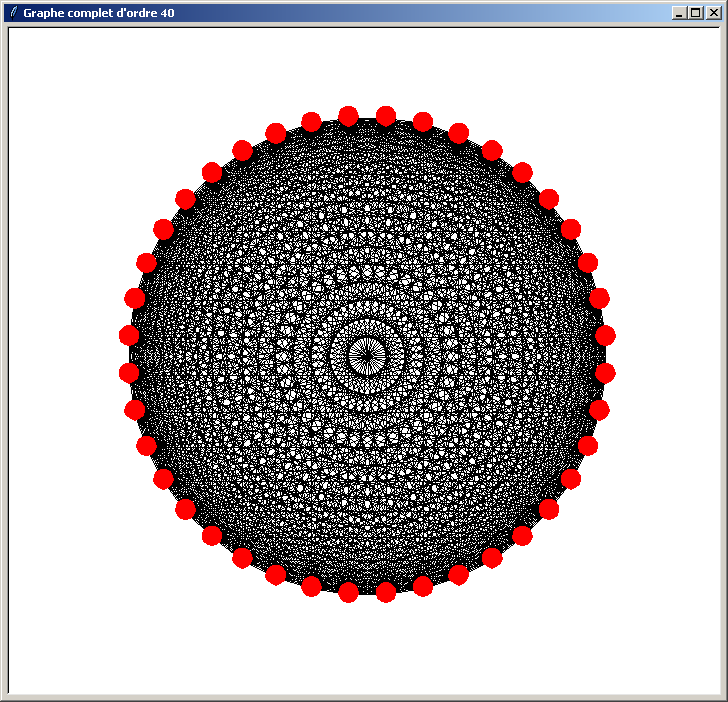
Le problème du programme précédent est qu'il n'est pas optimisé. Il perd du temps lors du traçage du graphe pour les raisons suivantes :

• il trace plusieurs fois la même arrête
• il dessine les sommets dans une nouvelle boucle for après avoir dessiné toutes les arrêtes

Le programme optimisé ci-dessous résoud ces problèmes :

• il trace une seule fois chaque arrête (bien plus rapide que la version de base pour les graphes d'ordre supérieur à 12)
• il dessine les sommets en même temps que les arêtes (dans la même boucle for)

Voici la version optimisée de cette SOLUTION 1 :

Graphe complet optimisé

SOLUTION 2 :

Cette SOLUTION 2 calcule mathématiquement les coordonnées et les angles entre les sommets (en utilisant le sinus, le cosinus, le nombre pi, etc.) et n'utilise pas la fonction position() de la tortue.

Voici le programme source en Python de cette SOLUTION 2 :

Graphe complet mathématique

Et voici le résultat obtenu pour un graphe d'ordre 9 :

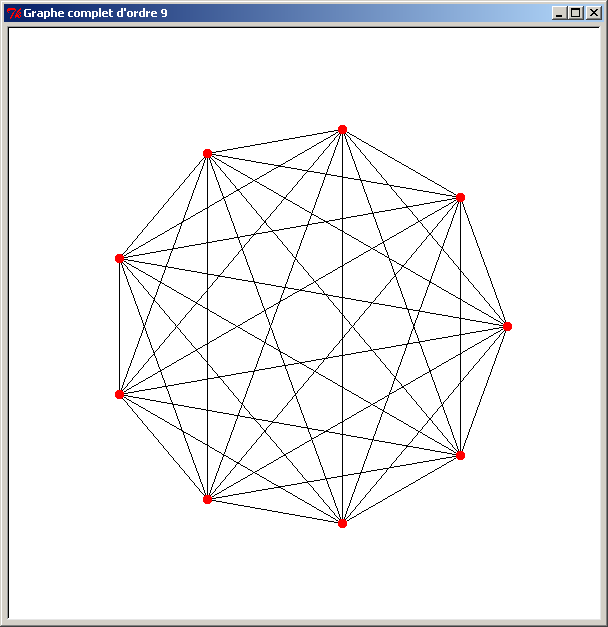
Exemple de graphe complet d'ordre 9

Pour évaluer vos connaissances acquises en Python, utiliser le QCM Python :