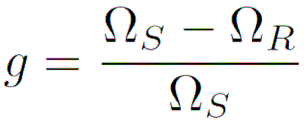Depuis le lundi 16 mars 2020 le lycée est fermé, jusqu'à nouvel ordre, mais le travail continue.
Concernant les Sciences de l'Ingénieur le fil conducteur du travail à faire à la maison est guidé par le calendrier des 8 devoirs du troisième trimestre connu depuis le lundi 09 mars 2020 :
Ces 8 devoirs basés sur les 8 derniers QCM transversaux ont avant tout pour but de faire une révision générale avant le bac, tout en y ajoutant les derniers cours complémentaires de l'année ainsi que des notions demandées fréquemment dans les sujets de bac.
Fiches pratiques disponibles en bas de cette page :
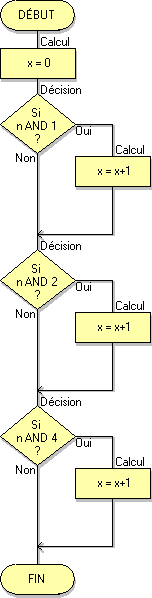
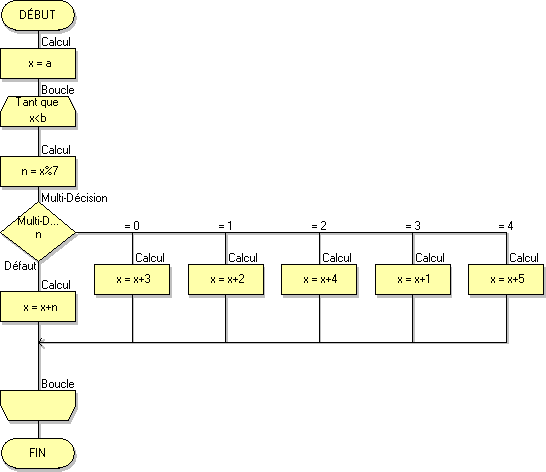
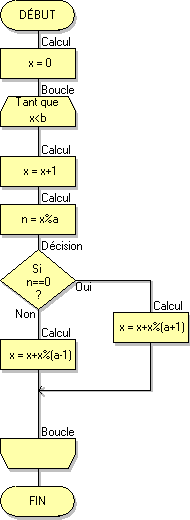
■ Les nouveaux algorigrammes Flowcode
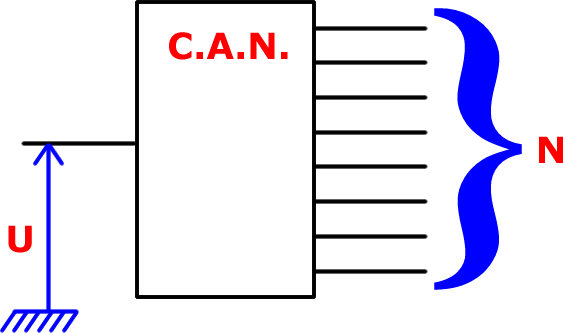
■ Les convertisseurs Numérique/Analogique et Analogique/Numérique
■ Les moteurs à courant alternatif
Principe et planification des devoirs du troisième trimestre :
■ les 8 devoirs sont connus depuis le lundi 09 mars 2020 et la date limite d'envoie des notes est le jeudi 4 juin 2020 à 22H00 pour tous les devoirs
■ les 8 notes seront remontées sur Pronote le jeudi 4 juin 2020 à 22H00, en même temps que la note bonus du troisième trimestre
■ vous avez donc plus de 12 semaines pour faire 8 devoirs : libre à vous de les planifier et de vous organiser
■ vous travaillez les 8 devoirs et vous envoyer les 8 notes rouges dans l'ordre que vous voulez
■ ATTENTION : toute semaine passée sans envoie de note rouge est une semaine perdue
■ idéalement on attend 1 note rouge par semaine (200 questions par semaine) afin de se "débarasser" des QCM dans 8 semaines
■ en cas de plusieurs notes rouges pour le même devoir on garde toujours la dernière note (identique pour les 8 devoirs)
■ pour plus de détails consulter les critères des devoirs
Contenu des QCM transversaux :
■ la majorité des questions posées dans ces 8 QCM transversaux font appel aux cours déjà vus, en première comme en terminale
■ certaines nouvelles questions ne feront pas l'objet de cours : à vous de prendre des notes et d'analyser ce qui est demandé
■ la liste des nouveaux types de questions présents dans les QCM transversaux et ne nécessitant pas de cours est donnée ci-dessous
■ certaines nouvelles questions doivent faire l'objet de cours complémentaires
■ ce sont ces cours complémentaires qui seront fait à distance, avant tout en mettant à votre disposition des ressources à consulter
■ la liste des nouveaux types de questions présents dans les QCM transversaux nécessitant un cours complémentaire est donnée ci-dessous
Particularité des QCM transversaux :
■ le QCM transversal n°2 (Devoir n°10) contient 8 thèmes fixes, tous connus, et qui ne se sont jusqu'à présent jamais mélangés
■ le QCM transversal n°3 (Devoir n°11) contient 4 thèmes aléatoires, tous connus, dont certains "thèmes mystères"
■ pour le QCM transversal n°3 vous ne connaissez pas à l'avance le contenu des "thèmes mystères", et si vous recommancez vous avez 4 nouveaux thèmes
■ les 2 QCM transversaux n°2 et n°3 ne sont pas inscrits dans les thèmes obligatoires : il ne peuvent donc pas remettre à zéro une jauge orange
■ les 6 QCM transversaux n°4 (Devoir n°12) à n°9 (Devoir n°17) sont des QCM à thème unique (pas de choix de thème au démarrage)
■ ils peuvent porter sur tous les thèmes vus en 2 ans, y compris des thèmes nouveaux, et vous ne connaissez pas à l'avance leur contenu
■ les 6 QCM transversaux n°4 à n°9 sont inscrits dans les thèmes obligatoires : il faut donc les utiliser pour remettre à zéro une jauge orange
■ l'idéal est que la jauge ne passe jamais à l'orange : envoyez régulièrement des notes vertes d'entraînement sur les QCM transversaux
■ pour les 6 QCM transversaux n°4 à n°9 on attend seulement 200 questions pour chacun : une seule note rouge suffit pour les équilibrer
Nouveaux types de questions présents dans les QCM transversaux et ne nécessitant pas de cours :
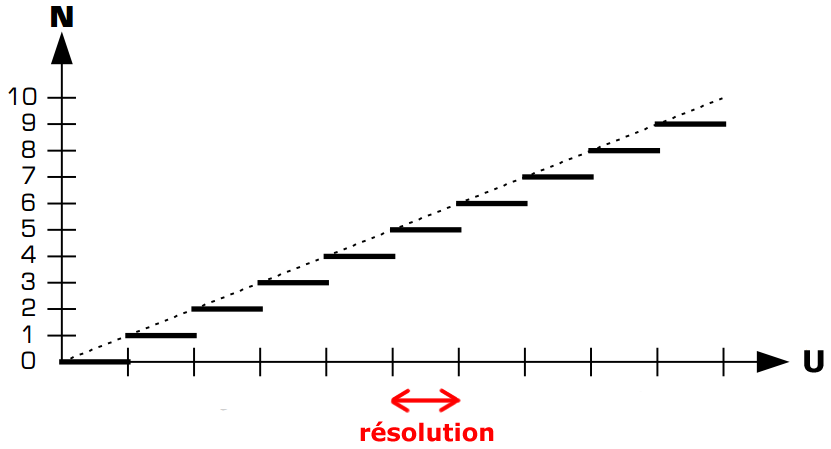
■ lecture d'un graphique
■ calcul du rendement global d'un système
■ calcul d'un écart relatif
■ analyse d'un algorithme
■ l'année de naissance des scientifiques dans l'histoire : ressource à consulter
■ maîtrise des unités de mesure de physique chimie (en plus des unités de sciences de l'ingénieur) : ressource à consulter
■ les différents types et les caractéristiques des batteries : ressource à consulter (page 23)
■ le protocole TCP/IP : ressource à consulter
Nouveaux types de questions présents dans les QCM transversaux et qui font l'objet d'une fiche pratique en bas de cette page :
■ codage binaire des nombres négatifs en complément à 2 : fiche pratique à consulter
■ les nouveaux algorigrammes sous Flowcode V4 : fiche pratique à consulter
■ les Convertisseur Analogique Numérique (C.A.N.) et Convertisseur Numérique Analogique (C.N.A.) : fiche pratique à consulter
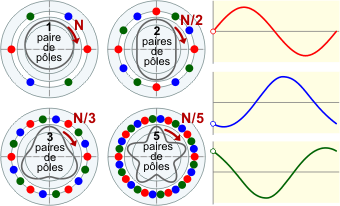
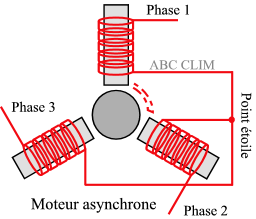
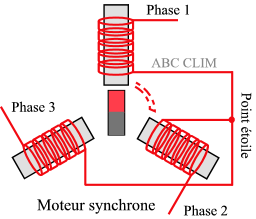
■ les moteurs à courant alternatif (moteur synchrone et moteur asynchrone) : fiche pratique à consulter
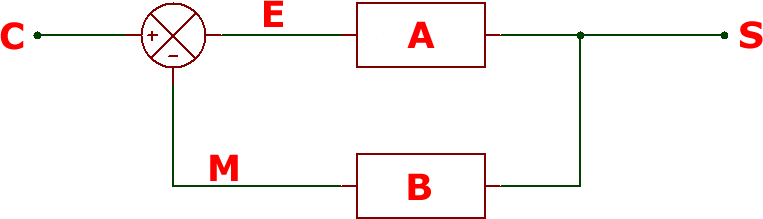
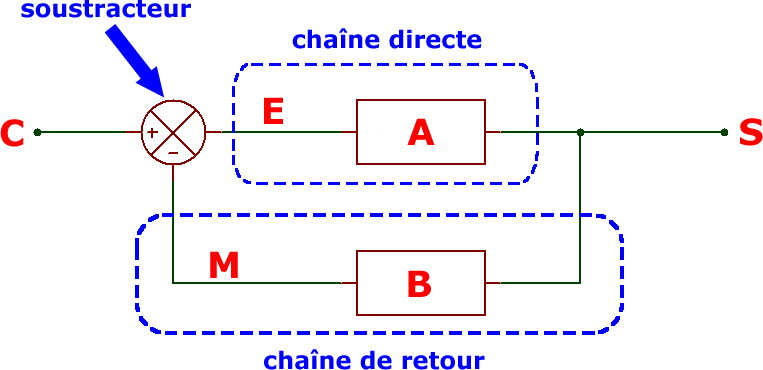
■ les systèmes asservis : fiche pratique à consulter ressource 2 à consulter ressource 3 à consulter
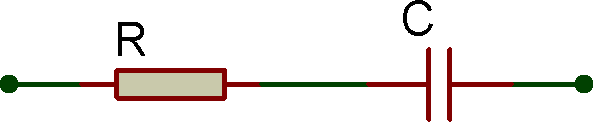
■ la bobine et le modèle RLE pour modéliser un moteur à courant continu : fiche pratique à consulter
Voici le contenu (non exhaustif) de chacun des 8 QCM transversaux :
| Seulement des thèmes connus (8 thèmes fixes) | ||
| Seulement des thèmes connus (4 thèmes aléatoires) | ||
Des thèmes connus avec en plus : ■ le complément à 2 ■ les C.A.N. et les C.N.A. |
||
Des thèmes connus avec en plus : ■ le complément à 2 ■ les C.A.N. et les C.N.A. ■ les moteurs à courant alternatif |
||
Des thèmes connus avec en plus : ■ le complément à 2 ■ les C.A.N. et les C.N.A. ■ la bobine et le modèle RLE |
||
Des thèmes connus avec en plus : ■ le complément à 2 ■ les systèmes asservis |
||
Des thèmes connus avec en plus : ■ le complément à 2 |
||
Des thèmes connus avec en plus : ■ le complément à 2 ■ les systèmes asservis |