Le thème Les algorigrammes utilisant les masques binaires du QCM "Algorithmes et algorigrammes" ne possède que 8 types d'algorigrammes. Certains d'entre eux existent en différentes variantes mais leur analyse reste la même.

Rappel :

Dans le thème Les algorigrammes utilisant les masques binaires, les masques binaires permettent d'effectuer un test sur les 3 bits de poids faible d'un nombre n : bits de rang 0, 1 ou 2 seulement.

Exemple de masques binaires pour différentes valeurs de n :

Voici les 8 algorigrammes commentés :

Algorigramme 1

Le test n AND 3 sera vrai si les 2 bits de poids faible de n ne sont pas nuls tous les deux (au moins un à 1)

Donc x vaut 1 si au moins un des deux bits de poids faible de n vaut 1, et 0 dans le cas contraire.

En clair x=0 si l'écriture en binaire de n finit par 00 : xxxxxx00, c'est-à-dire si n est multiple de 4

Algorigramme 2

Cet algorigramme existe en 2 variantes :

Dans les deux cas il suffit de remarquer que le test x XOR n est strictement équivalent à x est différent de n

A retenir : x XOR n sera nul seulement si x=n (principe du OU-Exclusif : la sortie est nulle si les entrées sont égales)

Algorigramme 3

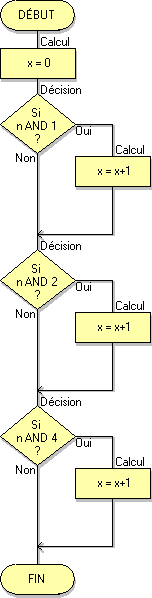
Le test n AND 1 est vrai si le bit de rang 0 de n vaut 1

Le test n AND 2 est vrai si le bit de rang 1 de n vaut 1

Le test n AND 4 est vrai si le bit de rang 2 de n vaut 1

On en déduit que cet algorigramme compte dans la variable x le nombre de bits à 1 parmi les 3 bits de poids faible de n

Exemples :

Si n = 0₍₁₀₎ = 00000000₍₂₎ alors x = 0

Si n = 1₍₁₀₎ = 00000001₍₂₎ alors x = 1

Si n = 2₍₁₀₎ = 00000010₍₂₎ alors x = 1

Si n = 3₍₁₀₎ = 00000011₍₂₎ alors x = 2

Si n = 4₍₁₀₎ = 00000100₍₂₎ alors x = 1

Si n = 5₍₁₀₎ = 00000101₍₂₎ alors x = 2

Si n = 6₍₁₀₎ = 00000110₍₂₎ alors x = 2

Si n = 7₍₁₀₎ = 00000111₍₂₎ alors x = 3

Si n = 8₍₁₀₎ = 00001000₍₂₎ alors x = 0

etc.

Il n'y a donc que 4 valeurs possibles pour x : 0, 1, 2 ou 3

Algorigramme 4

Le test i AND 1 est vrai si le bit de rang 0 de i vaut 1, c'est-à-dire si le nombre i est impair.

Le test i AND 1 est donc strictement équivalent à i est impair

Rappel : le test i XOR n est strictement équivalent à i est différent de n

Cet algorigramme compte donc tous les nombres impairs compris entre 0 et n.

Voici un algorithme sans masques binaires équivalent à cet algorigramme 4 :

Algorigramme 5

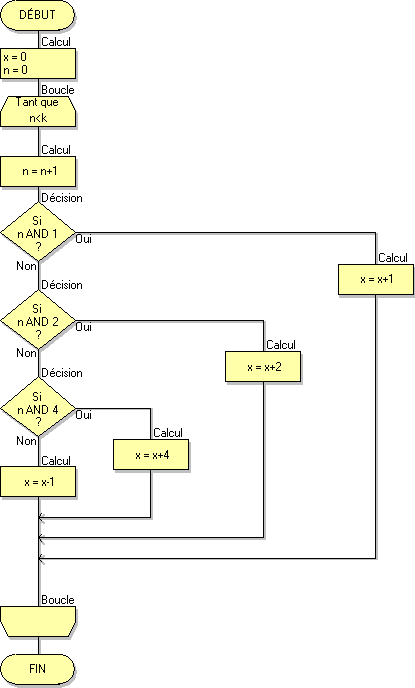
Test n AND 1 : si le bit de rang 0 du nombre n vaut 1 on ajoute 1 à la variable x

Test n AND 2 : si le bit de rang 1 du nombre n vaut 1 on ajoute 2 à la variable x

Test n AND 4 : si le bit de rang 2 du nombre n vaut 1 on ajoute 4 à la variable x

Enfin, si les 3 bits de poids faible de n sont tous nuls on enlève 1 à x : cas où on répond NON aux 3 tests

Algorigramme 6

Si i est impair on répond OUI au test i AND 1

Si i est pair on répond NON au test i AND 1

A retenir : le test i AND 1 est strictement équivalent à i est impair

On teste ici la parité des nombres compris entre 0 et b (intervalle de la variable i), 0 et b compris :

0 ≤ i ≤ b

Algorigramme 7

Cet algorigramme existe en 8 variantes

Pour les 8 variantes de l'algorigramme 7 la variable i est un entier compris entre 0 et b, 0 et b non compris :

0 < i < b     soit     1 ≤ i ≤ b-1

Dans les deux algorigrammes suivants on teste le bit de rang 0 de i (test i AND 1) ce qui revient à tester sa parité.

Le seule différence entre ces deux algorigrammes est la position des réponses OUI et NON dans le test :

Rappel : le test i AND 1 est strictement équivalent à i est impair

Dans les deux algorigrammes suivants on teste le bit de rang 1 de i (test i AND 2).

Le seule différence entre ces deux algorigrammes est la position des réponses OUI et NON dans le test :

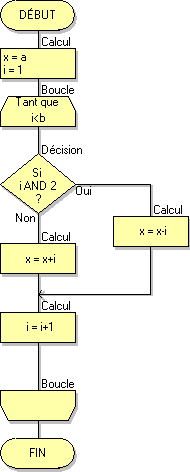
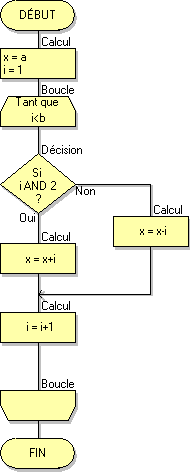
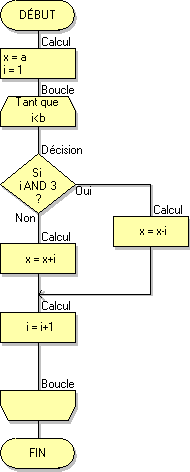
Dans les deux algorigrammes suivants on teste en même temps les bits de rang 0 et 1 de i (test i AND 3).

Rappel : le test i AND 3 est équivalent à i n'est pas un multiple de 4

Le seule différence entre ces deux algorigrammes est la position des réponses OUI et NON dans le test :

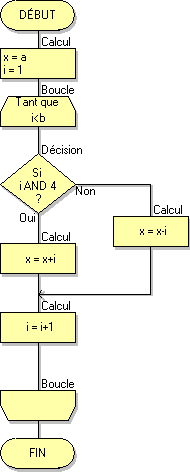
Dans les deux algorigrammes suivants on teste le bit de rang 2 de i (test i AND 4).

Le seule différence entre ces deux algorigrammes est la position des réponses OUI et NON dans le test :

Algorigramme 8

Cet algorigramme existe en 2 variantes

Le seule différence entre ces deux algorigrammes est la position des réponses OUI et NON dans le test :

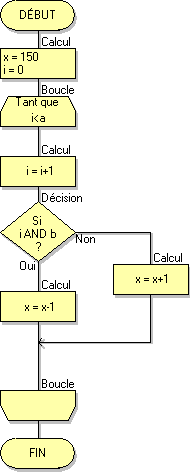
Par rapport aux 7 premiers algorigrammes, ici le masque binaire b est variable :

Si b=1 on teste le bit de rang 0 de i (détection des multiples de 2)

Si b=2 on teste le bit de rang 1 de i

Si b=4 on teste le bit de rang 2 de i

Et si b=3 on teste à la fois les bits de rang 0 et 1 de i (détection des multiples de 4)

La valeur de b qui est fixe est donnée dans la question et vaut soit 1, soit 2, soit 3, soit 4.

De plus la variable i utilisée dans le masque binaire est un entier compris entre 0 et a, 0 et a non compris :

0 < i < a     soit     1 ≤ i ≤ a-1

Pour aller plus loin

Dans la suite des nombres binaires, donnée dans le tableau ci-dessous, on peut remarquer que :

Le bit de rang 1 du nombre N vaut 0 si N est multiple de 4 ou si N est (un multiple de 4) +1

Et le bit de rang 2 du nombre N vaut 0 dans les 4 cas suivants :

Ces remarques permettent de déterminer rapidement par le calcul si les tests N AND 2 et N AND 4 sont vrais ou faux :

Réalisé par Jean-Christophe MICHEL

© Décembre 2020